Whatever happened to competition in space agency procurement? The case of NASA

Whatever Happened to Competition in Space Agency Procurement? 229

Figure 2. Recursive graphics

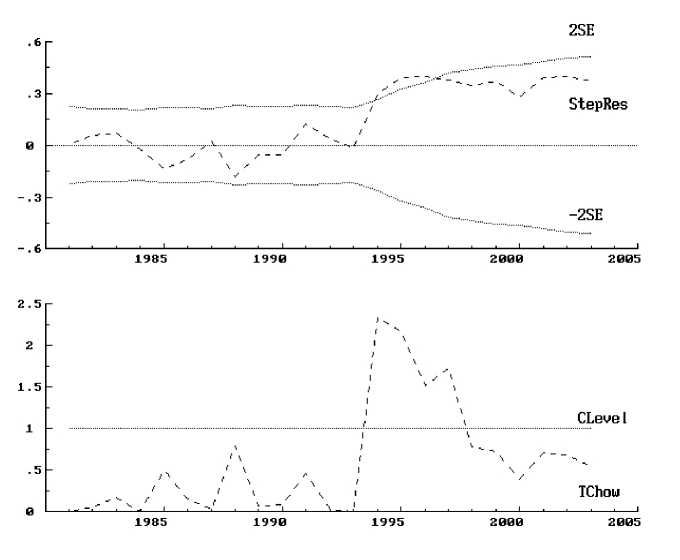
Notes: The recursive graphics are based on the recursive least squares (RLS) estimation
with LNASAnc as dependent variable and LSE_NASA and LNASAtop10 the independent varia-
bles. The use of the RLS method of estimation (see Doornik and Hendry, 1995) is chosen to
graphically illustrate the presence of structural breaks. The methodology employed by the
recursive method of estimation of a model for a sample with T observations is to apply
successive OLS estimates to the model starting with M observations (M<T), and then fit
the model to M+1, M+2,... up to T observations (Doornik and Hendry, 1995: 140). This way
a number of successive residual sums of squares are obtained based on which a sequence
of tests for structural breaks and parameter constancy can be conducted (ibid: 268). Two
graphics-based tests for parameter constancy are presented. The top graph presents the
one-step residuals test, where the one-step residuals of y_t - x_tβ_t (StepRes) are bordered
by plus and minus two standard deviations from M to T sample observations (2SE and -
2SE, respectively). Points outside the boundaries reveal coefficient changes. The lower
graph presents the one-step Chow test, which is based on one-step forecast tests (TChow)
following the F-distribution with 1, t-k-1 degrees of freedom for t=M,...,T and a null of
parameter constancy (Doornik and Hendry, 1995: 328). Points above a chosen (5%) level
of significance in the diagram (CLevel) reveal the time period for which the null is rejected.
Both graphs are for M=5 and reveal a major structural break in 1994, as expected.

<<   7   8   9   10   11   12   13   >>

More intriguing information