The fundamental determinants of financial integration in the European Union

(13)

β WG

N               1 - 1 Γ N

∑X'_iQX_i ∑ X₁QU

i = 1                                  i = 1

j∙ Euro

(14)

^i,.wa-O->'^s'"^,∖-×'JwG

(15)

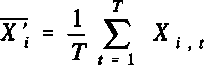
The variance-covariance matrix of the within-group estimator is

VÂR (P_ifg) = ô

N          1-1

∑x^,_iQx_i

i = 1

(16)

with

1         ^N

⁰= ⁼ NT λ,.H Σ I <ⁱ-ⁱ'^a,"^,)∣-W-^χ3≡ ]' [                    ]

IVx {1N+∣C) _{I =} J

and
^ 2

ʌ ʌ         — ʌ .     — σ _e

≡( c.w) (X_i VAX P_wg) X_i ⁺ -γ          (17)

The parameter k denotes the number of regressors. Basically, the fixed-effects model implies that all countries
have the same coefficients in front of the exogenous variables but that the intercepts are different among
the 11 EU countries. We are referring to the generalized country-specific effects (ζ_i) because we are only
able to estimate these in a composite form. This is no problem because our main interest is not in the exact
value of these effects but their ranking. Furthermore, under proper conditions for the error term we can

32

The estimator is called this way because only the variation within each group (country) is used.