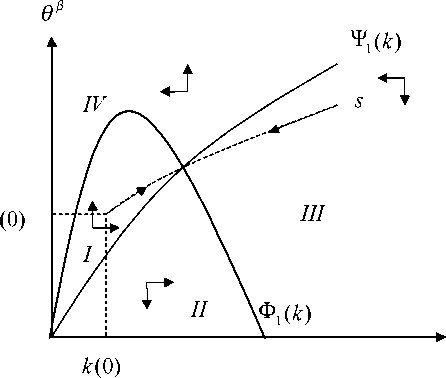
Qualification-Mismatch and Long-Term Unemployment in a Growth-Matching Model

Figure 4: Analysis of the Stability for the Steady-State.

dynamic factor allocation function¹⁷

θ^β =

(1 ^—^a^{) (1} — ^β (1 — ω) λ₀

^t⅛A (1+C∕)

k“-¹ + β(u — V) + v

— k".
λ

ʌ ʌ

Considering U = V =

ʌ

—θ, the function can be rewritten as

β 1 + C₁

k^a~¹ —

⁽¹^—^a^{) (1}^—^β⁽¹^—^ω) ʌo

ʌ
θ)θʌ

k^aθ~^β+ v

λ θ. (25)

Equation (25) shows the transitional dynamics for θ^β, i.e. labor market tightness
increases if

θ^β >

⁽¹^—^a^{) (1}^—^β⁽¹^— ш⁾ λ₀

Г -I k

ʌ ʌ

C_v0λ v — λ+ ɪkɑ-i

Thus, labor market tightness increases, if the realized level of labor market tightness
is greater than the equilibrium level and vice versa.

Furthermore, the following dynamic capital accumulation function can be derived

ЯЧ¹⁸

as

k= , '

1 + CjS

k^a

ʌo

— (λ + e) k.

(26)

¹⁷See appendix.

¹⁸For a detailed derivation see appendix.

21

More intriguing information

1. FUTURE TRADE RESEARCH AREAS THAT MATTER TO DEVELOPING COUNTRY POLICYMAKERS
2. The Role of State Trading Enterprises and Their Impact on Agricultural Development and Economic Growth in Developing Countries
3. Performance - Complexity Comparison of Receivers for a LTE MIMO–OFDM System
4. On s-additive robust representation of convex risk measures for unbounded financial positions in the presence of uncertainty about the market model
5. The name is absent
6. Wirtschaftslage und Reformprozesse in Estland, Lettland, und Litauen: Bericht 2001
7. The name is absent
8. The name is absent
9. DISCUSSION: POLICY CONSIDERATIONS OF EMERGING INFORMATION TECHNOLOGIES
10. IMMIGRATION AND AGRICULTURAL LABOR POLICIES
11. Skill and work experience in the European knowledge economy
12. Luce Irigaray and divine matter
13. The WTO and the Cartagena Protocol: International Policy Coordination or Conflict?
14. INSTITUTIONS AND PRICE TRANSMISSION IN THE VIETNAMESE HOG MARKET
15. The role of statin drugs in combating cardiovascular diseases
16. Methods for the thematic synthesis of qualitative research in systematic reviews
17. The Employment Impact of Differences in Dmand and Production
18. American trade policy towards Sub Saharan Africa –- a meta analysis of AGOA
19. Distribution of aggregate income in Portugal from 1995 to 2000 within a SAM (Social Accounting Matrix) framework. Modeling the household sector
20. FISCAL CONSOLIDATION AND DECENTRALISATION: A TALE OF TWO TIERS