The name is absent

*   (nɪ + n - 1)

⇒ τ =--------

a^*

is the constant tax that will achieve the Pareto-optimal amount of phosphorous
loading when each community acts to maximize its welfare in a non-cooperative
way.

3.7 Private Equilibrium with Tax

To determine the impact of the tax on the non-cooperative phosphorous loading
in steady state and on the state of the lake, λ(t), λ_i(t) and λ_j∙(t) is substituted
into the steady-state tax equation. Therefore substituting (14), (24) and (25)
back into (23) one obtains:

1        ⁿ¹                                        2x(t)

2---------Г I 2cix(t) + λi(t) b + p — ------------2 I

(nɪ + П2) ЁЛ              L       (x²(t) + 1)2J√

⁺ g ^2cCx x^{(t) + λ}j ^{(t) b + P} — _{2 2}/,ʌ(,) -, x2 ^λ)
j=Λ               L        ⁽x^{2(t) + 1)} ∖)

. ./,ʌ          2 /,ʌ 2/,_λ(ⁿ1^c1 ^{+ n}2^c2)

⇒ a(t) = -Cx(t)α (t)---------

(nɪ + n2)²

a²(t) Γ,           Cx(t)    ↑ n n^ ʌ   ^2   z Λ z ʌ

— 2-------πr b + P--λ   g λ_i(t) + g λj(t)  (C8)

(nɪ + n2)²[       (χ²(t) + i)²J y⅛ i^u  j=i jɪ ^!

From (C0)

^λi(^t) =^{τ -} oi(ty^{and λ}j^(t) =^{τ -} aj⅛t              ^(C9)

By substituting into (C8) one obtains:

n2
+ g

j=1

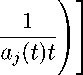
Recognizing the last two terms as -λ(n₁ + n₂) and substituting -(nɪ + n₂)∕α(t)

15

<<   14   15   16   17   18   19   20   >>

More intriguing information