Given a stronger theoretical validity than other location quotients and the latest empirical results,
the FLQ is applied in this analysis to estimate for every Romanian region the matrices of input and
total trade coefficients.
The FLQ takes the following form4:
FLQij =
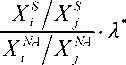
(6)
where λ* = pog2 (1 + XS/XNA )] , 0 ≤ δ < 1, NA refers to the nation. δ is a parameter that has to be
estimated5. The larger the value of δ , the greater the adjustment for regional imports. So, δ is
inversely related to the size of the region.
Starting from a 2000 13-sector national I-O table6, for a given region S, input coefficients matrix,
A SS = ∣^ aSS ], and total trade coefficients matrix,
A RS = ∣^ aR ], are derived as follows:
SS
ij
∫ r I'π
I rNA
I rj
if FLQiSj < 1
if FLQiSj ≥ 1
(7)
∫rjNA .(1 - FLQS ) if FLQS < 1
aiRjS=I
(8)
0 if FLQSj ≥ 1
where R expresses the rest of the country; rijNA is the national technology coefficient; aiSjS is the input
coefficient of region S; aiRj S is the total trade coefficient of region S and expresses the amount of
imports of good i (per unit of output j) to region S from the rest of the country.
The logic behind the above systems is that the relatively less important sector i than sector j in
region S and the relatively smaller region S ( FLQiSj < 1), the more the local production cannot satisfy
the entire local demand and a part of production will be imported from the rest of the country.
Technically, the national technology coefficient is reduced and the difference is attributed to the total
trade coefficient.
Otherwise, the relatively more important sector i than sector j in region S and the relatively bigger
region S ( FLQiSj ≥ 1), the more the local production can fulfil all local requirements and no goods and
services will be imported from the rest of country. In this case, the input coefficient of region S will be
given equal to the national technology coefficient whereas the total trade coefficient will be null.
4 The version elaborated by the authors uses employment data instead of output data. Employment data are generally
used when reliable data on output (or value added) are missing. In this research, we used output data estimated by applying
ratio between regional and national sector GDP to national output.
5 A value of 0.3 was assigned to the parameter δ . The FLQ’s authors demonstrated that this value can be good for
even very different regions (Flegg and Webber, 1997).
6 The available national I-O table was a 2000 34-sector Romanian I-O table expressed in basic values and reporting
domestic flows. Before regionalizing, first, national imports were reallocated within the secondary sectors of the national I-O
table to derive a technology matrix, as Jensen et al. (1979) suggest. Second, the national I-O table was aggregated into 13
sectors owing to the reduced availability of sector data at a sub-national level.