the market and other factors add more price variability around the trend. Therefore, this
stochastic trend model is also fitted to price data.
The model consists of one measurement equation and two transition equations:
(6)
yt = μt + εt
μt = μt-1+ βt—1+ ηt
βt = βt-1 +ςt
where yt is the independent variable indexed by time t ;
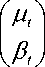
is the state vector; εt is the random
error describing the short run randomness with mean zero and variance σε2 ;3
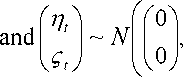
2
ση
I 0
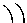
σ2
is the error vector describing the long run randomness in the
transition equation that governs the evolution of the state vector. Both of the errors in the
measurement equation follow normal distributions and are independent of each other.
In the basic specification, μt, the mean component of the dependent variable, is shown
as a random walk with a drift. Therefore the final generalization shows that the mean of the
dependent variable grows at a random rate.
3 The model also allows for a non-normal errors when εt is assumed to be generated by an inverse
hyperbolic sine transformation from normality: et= (τt-δ)~N(0,1), and
τt =θ-1 ln θεt+
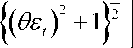
where δ is the non-centrality parameter; δ > 0(< 0) denotes the
distribution is skewed to the right (left) and if δ = 0 the distribution is symmetric. θ is associated with
the degree of kurtosis with θ ≠ 0 denoting a kurtotic distribution. Thus, the error term can be expressed
as εt
eθτt
e-θτt
2θ
12
More intriguing information
1. TOWARD CULTURAL ONCOLOGY: THE EVOLUTIONARY INFORMATION DYNAMICS OF CANCER2. The name is absent
3. The Importance of Global Shocks for National Policymakers: Rising Challenges for Central Banks
4. CHANGING PRICES, CHANGING CIGARETTE CONSUMPTION
5. IMPACTS OF EPA DAIRY WASTE REGULATIONS ON FARM PROFITABILITY
6. Modellgestützte Politikberatung im Naturschutz: Zur „optimalen“ Flächennutzung in der Agrarlandschaft des Biosphärenreservates „Mittlere Elbe“
7. Valuing Farm Financial Information
8. Self-Help Groups and Income Generation in the Informal Settlements of Nairobi
9. The name is absent
10. The name is absent