11
5. Spatial autocorrelation
In advance to estimation und testing Moran’s I is computed as an overall measure for
spatial autocorrelation for the variables considered. For the Okun relation, the FD speci-
fication is preferred, as it is based on observables. For all variables, the Moran coeffi-
cient fluctuates over time (see Figure 5.1). However, in most years spatial dependencies
are striking in every case. With the exception of GDP growth in 1997 and 1999,
Moran’s I is significant at least on the 5 per cent level.2
As spatial autocorrelation varies over time, it will be not be removed by uniformly ap-
plying Griffith’s filtering method to the variables over the entire sample period. This
view is supported by the distinct map patterns in individual years. Although some
common spatial components of the variables are at work over time, other eigenvectors
of the C matrix change their significance from year to year. Hence, a varying spatial
pattern has to be taken into account.
Figure 5.1: Moran’s I of georeferenced variables
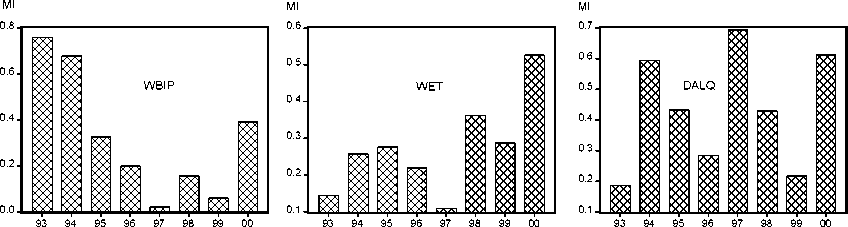
GDP growth Employment growth Unemployment (FD)
The spatial SUR model (3.4) presupposes that the explanatory variable is independent
from the error term.3 Thus GDP growth is pre-filtered to remove spatial effects. The
growth rate of employment and the change of the unemployment rate are explained by
the spatially filtered GDP growth rate and the map patterns of the endogeneous vari-
ables, that are extracted from the C-matrix. The spatial autocorrelations of the candidate
2 The significance of Moran’s I holds for both approaches randomisation and normal approximation.
3 The issue of exogeneity of output in Verdoorn’s hypothesis is addressed by Fingleton (2000) in a spatial
lag model. Though the Hausman test provides some evidence for endogenous output, due to indetermi-
nateness Fingleton favours output to be treated as exogenous.
More intriguing information
1. The Impact of Hosting a Major Sport Event on the South African Economy2. Gender and aquaculture: sharing the benefits equitably
3. Real Exchange Rate Misalignment: Prelude to Crisis?
4. A multistate demographic model for firms in the province of Gelderland
5. Transgression et Contestation Dans Ie conte diderotien. Pierre Hartmann Strasbourg
6. Knowledge, Innovation and Agglomeration - regionalized multiple indicators and evidence from Brazil
7. The name is absent
8. The name is absent
9. Public Debt Management in Brazil
10. TOWARD CULTURAL ONCOLOGY: THE EVOLUTIONARY INFORMATION DYNAMICS OF CANCER