Thresholds for Employment and Unemployment - a Spatial Analysis of German Regional Labour Markets 1992-2000

12

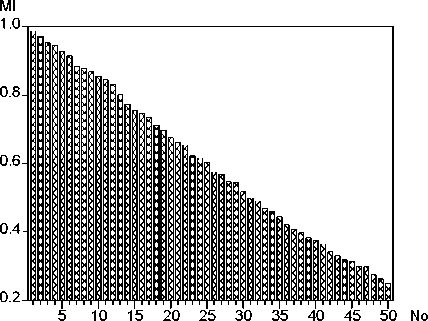
eigenvectors for forming those map patterns are exhibited in Figure 5.2. MI_max takes a
value of 0.988. According to the MIMI_max criterion the number of relevant eigenvectors
is restricted to 50.

Figure 5.2: Moran’s I of candidate eigenvectors

The map patterns of the eigenvectors corresponding to the eight largest eigenvalues of
the C-matrix are portrayed in Figure 5.3. As expected there exist only a very limited
number of clusters which increases with a decreasing degree of positive spatial autocor-
relation. The clusters appear to lie on trend surfaces with positive or negative gradients
depending upon the arbitrary chosen starting point. Obviously, a smooth transition from
high-valued to low-valued clusters and vice versa takes place in the case of strong spa-
tial autocorrelation. With a decreasing degree of positive spatial autocorrelation the map
pattern becomes more speckled.

While eigenvectors extracted by principal component analysis may (PCA) have an eco-
nomical significance, the eigenvectors of the C-matrix represent purely spatial compo-
nents which may be accessible to a geographically interpretation (for methodical simi-
larities between spatial filtering and PCA see Griffith, 2002, pp. 93). The map pattern of
the eigenvector corresponding with the largest eigenvalue suggests itself to interpret the
first spatial component as north-south component, since its trend surface shows a clear
north-south inclination. Analogously, we can speak of the second spatial component as
a west-east component. For the third and forth spatial component in each case two trend
surfaces appear to exist: one having an east-west inclination in the northern and the
other having an slope in the opposite direction in the southern part of the country. The

<<   9   10   11   12   13   14   15   >>

More intriguing information