that Ti is a Markov time with respect to the filtration Tτi-ι∙ The likelihood of
the sample can be written in compact form as:
N T
ь(^) = ППРг{^Ы} =
i=l t=l
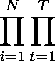
√¾λh,∙m⅛J' *»1»
1 ÿi,i / ∙ yt,τ ɪ yt,t
where p⅛ι⅛ is given by (8), and is therefore a function of sʤi-i and the parameters
7∙
Under some conditions, developed in the following, maximization of the log-
likelihood leads to consistent, asymptotically normal and asymptotically effi-
cient estimates of the parameters of the model, which ensures that LR tests are
asymptotically χ2 distributed under the null hypothesis.9 Let us discuss the
asymptotics involved, by considering three cases:
• T —> ∞, N finite
• T finite, N —> ∞
• T —> ∞, T —> ∞
To keep the notation simple, notice that the Markov model for homogeneous
population can be written in a compact notation, since it is equivalent to a
Markov model for the process {St} which, at any time t, takes on values in
a finite state-space 5 = {0,1,2,3},1° with a stationary (or time-homogeneous')
transition probability matrix P = ∣∣F⅛j⅛11, (h,k) & S×S; clearly F is a stochastic
matrix, that is, F⅛⅛ ≥ 0 Vh, k, and ɪ) ?hk = ɪ- Moreover we define
fees
F" = F-^=∣∣F^∣∣
n times
where Pf{k = Pr {St+n = k∖St = h}.
Essentially, what we need to have the usual asymptotic properties for the
ML estimates and LR tests is that all the transitions whose probabilities have
to be estimated (i.e. are not known) can be observed infinitely many times
as T and/or N go to infinity. It is intuitive that this ensures consistent and
asymptotically normal estimates of the transition probabilities. This requires
the following:
9McFadden (1984) proves consistency and asymptotic normality for a general multinomial
model under more general conditions, but the extension in this case seems to be difficult,
because he postulates that the explanatory variables are independent identically distributed for
each observation. This does not seem to hold generally for multiperiod models; nevertheless,
McFadden’s result can be applied to our homogeneous model.
10The elements of S correspond element-wise with the elements of У, so defined:
У = {(0,0), (0,1) , (1,0) , (1,1)} .
representing the state space of the process {Yi} at any time t.
12
More intriguing information
1. The effect of classroom diversity on tolerance and participation in England, Sweden and Germany2. Assessing Economic Complexity with Input-Output Based Measures
3. Qualification-Mismatch and Long-Term Unemployment in a Growth-Matching Model
4. Qualifying Recital: Lisa Carol Hardaway, flute
5. Peer Reviewed, Open Access, Free
6. Two-Part Tax Controls for Forest Density and Rotation Time
7. Education Responses to Climate Change and Quality: Two Parts of the Same Agenda?
8. Opciones de política económica en el Perú 2011-2015
9. The name is absent
10. Innovation in commercialization of pelagic fish: the example of "Srdela Snack" Franchise