The name is absent

∞          ∞

R[d] ʃ^ a [pr] ∫Ψ[ w] dwdpr

0            W [pr,d]

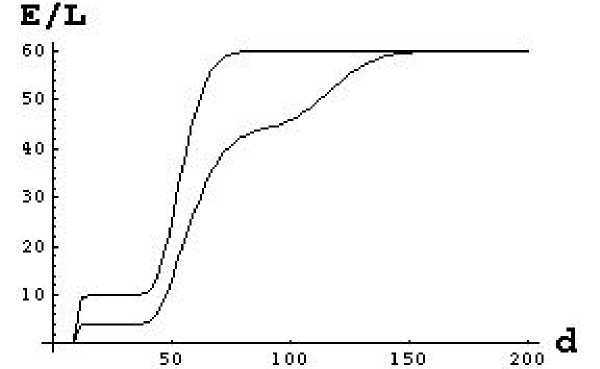
Figure 6

Fractions of Employment/Labor as a
function of traveling distance d to CBD

The possibility of multipurpose
shopping represents a centripetal force
that attracts customers to the city
center. Figure 6 illustrates the effect of
this force. The upper curve refers to a
situation where only one type of good
is considered. The lower curve
indicates how the propensity to do their shopping locally is reduced for customers with residence
outside the city center.

Using the set of ideas above, we are also able to include various other effects in our model. One such
aspect is an increased willingness to travel to the CBD during weekends, which may partly be
explained through a tendency to put less weight on the time consumption part in this case. Any
particular service may be split into 7 daily services, the time component part can be allowed to vary
on a daily basis. The local sector activities are then reproduced using a weighted average of the
expression (2.3).

If we interchange the order of integration in (2.3), we get
(2.4)

R [ d] ɪʃ   ʃwΦ ( pr) dpr Ψ( w) dw

00

where TC=TC[w,d] is the generalized traveling cost for traveling a distance d when the wage level is
w . Differentiating this expression, we see that

(2.5)

R'[d] = ʃΦ_a (TC[ w, d]) ^aTCj w, d^] dprΨ(w) dw

I a^      ∂d

If we assume that the mapping d→ TC[w,d] is linear or more generally concave, we get
(2.6)

∞

R''[d] ≤∫Φa(TC[w,d])PTj.^V, ]
о              <   ^ad

<<   6   7   8   9   10   11   12   >>

More intriguing information