10
Figure 6. Object with scale-range (left): the object is only visible when the view is within its scale-range;
Semantic zooming (middle): the object has different representations at different scales (simple square at
low scale, simplified outline at medium scale, complete detail at high scale) ; Scale-independent beacon
(right): below a certain scale, the object is always visible and has a fixed display size.
3.2. Modeling Multiscale Pointing
Pointing at a target in a multiscale document can be modeled with the same variables as with
a regular document: target distance D and target size W. As with traditional Fitts’ pointing
tasks, we can reduce the problem to a single dimension, and therefore use space-scale
diagrams with one dimension of space (horizontal) and one dimension of scale (vertical).
Figure 7 shows the three points that define a pointing task in a space-scale diagram. The
starting point (left) and the edges of the target (right) are represented by three great rays. If we
consider the pointing task at different scales (scales a, b and c in Figure 7), we observe that
the index of difficulty is scale independent since the ratio D/W is invariant. Therefore one can
vary the scale of the task for a fixed ID and study the effect of scale on pointing performance
(Guiard, 2001; Accot & Zhai, 2001).
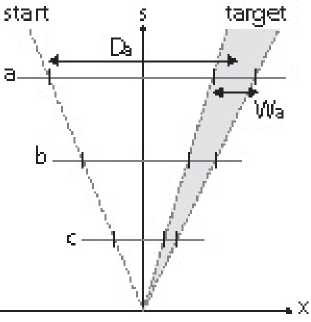
Figure 7. A Fitts task shown at three different levels of scale (a, b and c), using the 1D version of Furnas
and Bederson’s space-scale diagram. Whatever the scale, the ratio of target distance to target width
(Da/Wa, Db/Wb, Dc/Wc) is constant. Db, Wb, Dc and Wc are not shown for readability.
At very low scale, the displayed amplitude becomes so small, say less than a pixel, so as to
render the task impossible. At a very large scale, the viewing window cannot include both the
starting point and the target, and therefore the user has to use view navigation in order to
acquire the target. Finally, even if the view includes both the starting point and the target, it
may be impossible to select the target if it is too small relative to the view, e.g. smaller than a
pixel. This occurs for high values of the D/W ratio, i.e. for large IDs. In summary, pointing a
target in a multiscale document generally requires view navigation and is therefore
qualitatively different from traditional pointing. For this reason, we call it multiscale
pointing.
The question then is whether or not multiscale pointing is subject to Fitts’ law. As we have
seen above, multiscale pointing can be defined with the same independent variables as
traditional pointing: target distance D and target width W. Space-scale diagrams suggest a
related set of independent variables to study multiscale pointing: scale and difficulty. The
scale of the task corresponds to its absolute amplitude D, while its difficulty corresponds to its
relative amplitude D/W. As shown in Figure 7 above, we can vary the scale of a task without
varying its difficulty. Figure 8 below shows that, conversely, we can vary the task difficulty
More intriguing information
1. Types of Cost in Inductive Concept Learning2. A Study of Adult 'Non-Singers' In Newfoundland
3. Incorporating global skills within UK higher education of engineers
4. AN EMPIRICAL INVESTIGATION OF THE PRODUCTION EFFECTS OF ADOPTING GM SEED TECHNOLOGY: THE CASE OF FARMERS IN ARGENTINA
5. LOCAL PROGRAMS AND ACTIVITIES TO HELP FARM PEOPLE ADJUST
6. BARRIERS TO EFFICIENCY AND THE PRIVATIZATION OF TOWNSHIP-VILLAGE ENTERPRISES
7. Chebyshev polynomial approximation to approximate partial differential equations
8. Innovation Policy and the Economy, Volume 11
9. The name is absent
10. Nurses' retention and hospital characteristics in New South Wales, CHERE Discussion Paper No 52