Target Acquisition in Multiscale Electronic Worlds

21

Zooming
Amplitude

Figure 18. Mean zooming amplitude as a function of task difficulty for ID = 8 bits, shown with 95%
confidence intervals.

Movement Time

We defined MT as the amount of time elapsed between two consecutive hits. As shown in
Figure 19, the mean MT vs. ID curve was almost perfectly modeled by the usual version of
Fitts’ law, namely, ID = log₂ (D/W +1) (see Soukoreff & Mackenzie, this issue). A linear
regression yielded MT = 0.32 ID - 0.04, r² = .995, with all seven participants displaying a
very good linear fit (.981<r²<.999). Keeping in mind that we used data points spread over a
very wide-ranging selection of IDs, such a fit is remarkable.

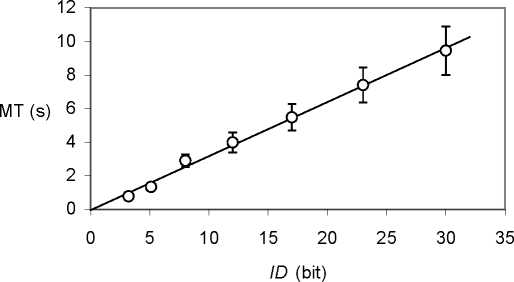
Figure 19. Fitts’ law assessed over a selection of IDs ranging far beyond 10 bits, due to the zooming
function.

Fitts’ law intercept was close to zero (0.04 s on average), consistent with our prediction of the
simplest possible version of the law, of the form MT = k * ID.

Zooming-Out and Zooming-In Time

We parsed MT into zooming-out time (Z_oT), the time separating a successful click from the
subsequent peak of zoom-out (Z_min) and zooming-in time (Z_iT), the time separating a peak of
zoom-out from the subsequent hit. Recall that while Z_oT corresponded to a virtually pure
zooming time (with little or no panning), Z_iT represented the duration of a composite process
made up of a series of intricately alternating pans and zooms, which started almost
systematically with a large-scale pan.

<<   18   19   20   21   22   23   24   >>

More intriguing information