Target Acquisition in Multiscale Electronic Worlds

22

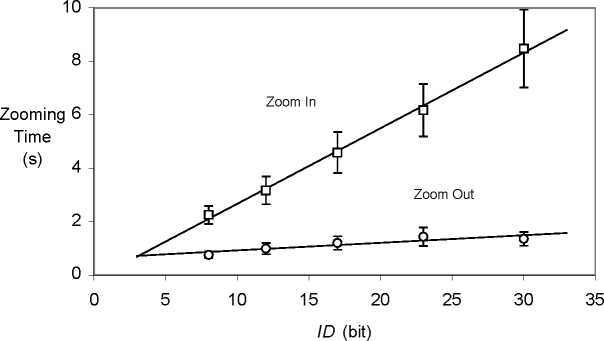
Figure 20. Mean zooming-out and zooming-in time as functions of task difficulty.

As shown in Figure 20, most of the time elapsed between two consecutive hits consisted of
Z_iT, with the initial zoom-out phase accounting for a vanishing proportion of MT as task
difficulty increased. Both components of MT were linearly dependent on the ID, but with
markedly different slopes (Z_iT = 0.28 ID - 0.16, r² = .997, and Z_oT = 0.03 ID + 0.63, r² =
.809).

Index of Performance

Fitts (1954) proposed using the ratio ID/MT, referred to as the index of performance (IP), to
quantify the rate of information transmission, or channel bandwidth, in the spirit of Shannon’s
information theory. Fitts’ first hypothesis was that the IP (dimensionally, in bit/s) should be
invariant along the continuum of task difficulty, but his own data showed the IP to vary with
task difficulty, as has been usually found in Fitts’ law research ever since (Soukoreff &
MacKenzie, this volume; Zhai, this issue).

Consistent with previous observations, the IP declined from the first to the second level of ID,
in the lower region of the difficulty continuum where the participants were better off without
the zoom (see Figure 21). This effect, evident in each individual participant, was highly
significant. For the higher five levels of difficulty, which required zooming, no more decrease
in the IP was obtained. On the contrary, we observed a slight but significant improvement of
the IP as pointing became more difficult (F(4, 24) = 10.38, p = .00005). However, this effect
was essentially due to the IP value at 8 bits being located lower than the other four—an effect
that presumably reflects the sub-optimal size of the screen we used. So, focusing on the 12- to
30-bit range, it seems fair to conclude that in this experiment the processing rate, or
throughput for multiscale pointing was essentially insensitive to task difficulty, in keeping
with Fitts’ (1954) initial expectation and our model.

<<   19   20   21   22   23   24   25   >>

More intriguing information