Artificial neural networks as models of stimulus control*

Response

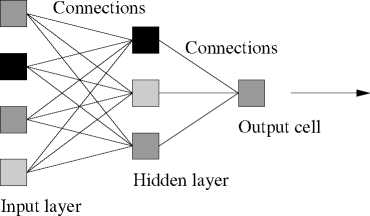
Figure 1: Schematic representation of a three-layer perceptron. Stimulation is assumed to
act on the units in the input layer (whose activation is illustrated as the degree of filling),
and is then transmitted to the middle layer (called the ‘hidden’ layer) via a system of
connections. These can amplify or reduce the signal. The same steps are repeated when
the signals travel from the hidden layer to the output cell, whose activation is the response
of the network to the stimulation.

stimulus control. Phenomena such as generalization and supernormal stimuli are
emergent properties. In addition, they are not ‘black-box models’: they consider
the architecture of the nervous system.

The aim of this study is to investigate in some detail how certain popular arti-
ficial neural network models generalize and compare these results with empirical
data. We shall not be concerned with a quantitative agreement, but rather we want
to see if these models are able to reproduce qualitatively a number of generaliza-
tion phenomena that are important in understanding animal behaviour.

2 The Model

We shall use three-layer artificial neural networks with the feed-forward archi-
tecture, also called multi-layer perceptrons (see e.g. Haykin, 1994), as shown in
figure 1. The input layer can be thought as modelling a perceptual organ, with
each unit i having an activation si in the interval [0, 1] when the stimulus s is pre-
sented to the network. The output of each hidden-layer cell is a function of the
weighted sum of such activations:
where N is the size of the input layer, w is the set of connections between the input
and hidden layers. The function φ(∙) is often referred to as the transfer function;
it describes the output of a unit given all its inputs, and it is usually a sigmoid

<<   1   2   3   4   5   6   >>

More intriguing information