Ultrametric Distance in Syntax

A

h=3

h=2

h=1

h=0

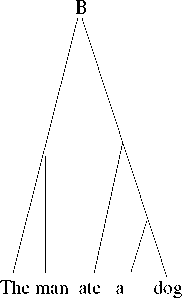
Figure 1: Different syntactic descriptions of “the man ate a dog”

However if the triangle inequality (4) is replaced by

Mxy ≤ max{Mxz, Mzy}.                      (5)

then M is an ultrametric, equation 5 implies 4.

1.3 Syntactic Phrase Trees

For the analysis of syntactic phrase trees the necessary technique is quite simple
and is illustrated by the examples in section 2. Psychological analysis of phrase
trees has been carried out by Johnson (1965) [18] and Levelt (1970) [22]. The
examples here mainly follow the examples in Lockward (1972) [23], Kayne (1981)
[20], McCloskey (1988) [24], and especially Haegeman (1994) [13]. There are at
least five reasons for introducing an ultrametric description of syntax.

The first is to completely specify tree (also called dendrogram) structure.

Consider the following example illustrated by Figure 1:

For current syntactic models the two trees usually are equivalent (perhaps
not always McCloskey (1988) [24] footnote 6): however consider the ultrametric
distance between ‘the’ and ‘man’,

A(the, man) = 1,     B(the, man) = 2,                 (6)

where the numbers are the height of the lowest common node above the two
lexical items. This ambiguity does not occur in current syntactic models, and
a purpose of an ultrametric model is to disambiguate the difference in height,
because this might have consequence in the complexity of the encoded model,
see the next point.

The second is it gives a measure of the complexity of a sentence: the greater
the ultrametric distance required the more complex a sentence is. The above
can also be viewed in terms of ‘closeness’. The example figure (1) illustrates that
current syntactic models give no notion of how ‘close’ determiners and nouns

<<   1   2   3   4   5   6   >>

More intriguing information