σ=
n
∑ ∣n X
i =1 xmin
-1
α-1
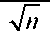
(6)
In the other hand, we also use the method of fitting is the standard method of Least Squares
Fitting (LSF) in the log-log scale of the data points as a comparative.
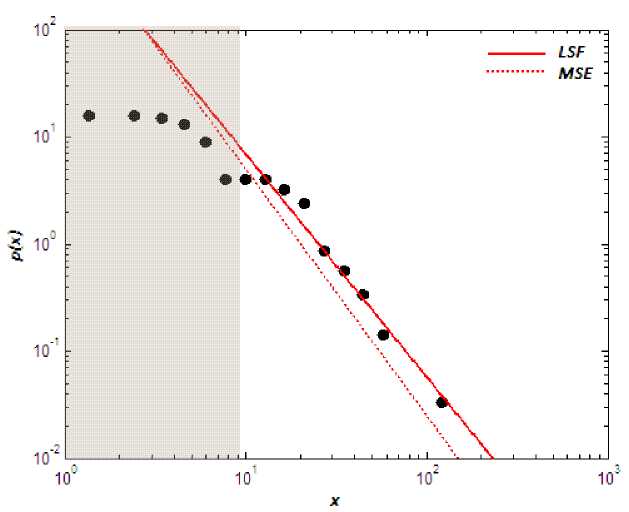
Figure 4. The power-law in the distribution of the casualties in Ambon Conflict 1999-2004. The shaded area is
the part of the data not included in fitting process as we use the value of Xmin = 9.9623.
Table 1. The fitting with MSE and LSE method.
|
__________α__________ | |
|
_________MSE_________ |
2.3176 ± 0.3196 |
|
______________LSF______________ |
2.0827 |
The result of the fitting process is shown in table 1 and figure [4]. In order to confirm
more about the power law, it is also shown in figure [5] the fitting value of the distribution
function with the real data. It is obvious that the data is attracted to the power law fitting
line of those variables we calculated.
As it has been observed by Moura, et. al. (2006), in general, the fitting exponent by
using the MSE is bigger than the one resulting from the LSF method. However, our main
concern is that by using both fitting methods, we found that the power law exponent is
approximately ≈ 2 with good fitting result ( R = 0.9836 ).This fact interestingly confirms the
Richardson law, that the power law is also appeared in the local wars - not only within the
More intriguing information
1. The Role of area-yield crop insurance program face to the Mid-term Review of Common Agricultural Policy2. Cardiac Arrhythmia and Geomagnetic Activity
3. A Note on Productivity Change in European Co-operative Banks: The Luenberger Indicator Approach
4. APPLICATIONS OF DUALITY THEORY TO AGRICULTURE
5. The name is absent
6. Portuguese Women in Science and Technology (S&T): Some Gender Features Behind MSc. and PhD. Achievement
7. The name is absent
8. The name is absent
9. The name is absent
10. An Efficient Circulant MIMO Equalizer for CDMA Downlink: Algorithm and VLSI Architecture