wars of the world. There have been such micro processes in the social system that emerged
the bird’s eye view of this interesting statistical feature. However, our discussions would
eventually approach possible micro process in civil violence or local massive conflict (that is
related to certain collective identities) yielding such multiplicative process of the casualties.
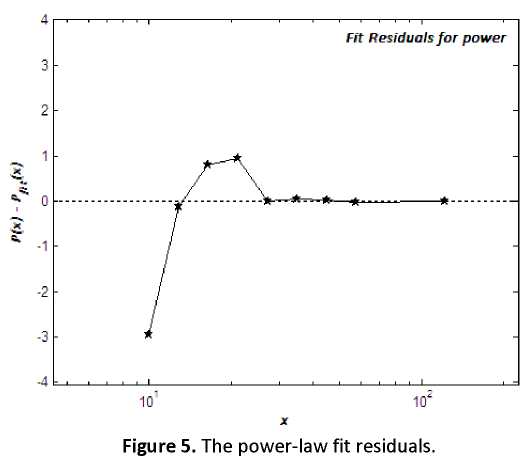
Interesting statistical facts from this finding are however the value of the moments
since power laws always bring non-statistical Gaussian properties. Since the exponent is
2<α<3 we can say that the first statistical moment (mean) does not diverge as if α= 1 .
The value of μ=< x > would settle down to a finite value in the limit of large data set. We
can write down the value of the first moment as
<x >=
∞
xp(x)dx =A ∫
xmin
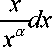
x-(α-2)
α - 2
xmin
(α-1) x
(α-2)
(7)
However, the second moment (mean square) can be written as
x2
x-(α-3)
(α - 3)
(8)
xmin
and reading the findings of the fitted exponent, we could say that the second moment of
the data would diverge in infinite value as the data set is larger. This is interesting feature
though, for theoretically speaking the ranges of the possible number of casualties in any
social clashes become ill-defined as we draw more and more samples into infinity.
Furthermore, from the derivation of Newman (2005), we could see that the
theoretical largest value with this interval of power law exponent,
More intriguing information
1. The name is absent2. Fiscal Reform and Monetary Union in West Africa
3. Multifunctionality of Agriculture: An Inquiry Into the Complementarity Between Landscape Preservation and Food Security
4. Detecting Multiple Breaks in Financial Market Volatility Dynamics
5. Consumption Behaviour in Zambia: The Link to Poverty Alleviation?
6. Evaluating the Success of the School Commodity Food Program
7. Accurate and robust image superresolution by neural processing of local image representations
8. The name is absent
9. DISCUSSION: ASSESSING STRUCTURAL CHANGE IN THE DEMAND FOR FOOD COMMODITIES
10. Internationalization of Universities as Internationalization of Bildung