1.2 Multi-Objective Optimization
Similar to coevolution, Multi-Objective Optimization (MOO)
involves a class of problems where a solution’s fitness is
contextually dependent on who the solution interacts with
during fitness evaluation. For example, consider a fitness
function defined based on linear ranking, e.g. where pair-wise
comparisons are used to count the number of solutions in a
population that a particular solution dominates. The fitness
function is shown in (1) where the population size is μ. Here
we use the standard connotation of the term dominance, where
one solution xi dominates another xj if the solution is better than
another in at least one objective and is equal or better in all
other objectives [11].
F(xi) = rank(xi) = ∑ dom(xi, xj
j≠i,j∈μ
(1)
Like coevolution, there are situations in MOO where the
relative viability (e.g. ranking order) of two solutions can flip
depending on the other solutions in the population. This is
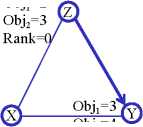
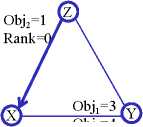
illustrated in Figure 1 where two solutions, X and Y, are being
compared to a third solution Z based on two objectives, Obj1
and Obj2. In Figure 1a, solution Z is only dominated by Y,
while in Figure 1b solution Z is only dominated by X. From
this simple illustration, one can see that dominance ranking in
MOO can be sensitive to the context (e.g. the definition of Z).
From hereafter, we define strong/weak contextual sensitivity of
a fitness evaluation based on the occurrence of different
contexts that can/cannot change the rankings of individuals.
Obj1=2
Obj2=4
Rank=1
Obj1=5
Obj2=2
Rank=O
Rank=1
Obj1=4
Obj2=4
Rank=0
a) b)
Figure 1: Contextual dependence of dominance ranking.
Dominance is indicated by directed connections.
Although Figure 1 illustrates how a strong contextual
sensitivity is possible in MOO, it does not tell us whether
strong sensitivity is commonly observed or whether it is
relevant to the dynamics of a multi-objective EA (MOEA) in
practice. If the contextual sensitivity is weak in MOO, then
changing the context for fitness evaluation will not morph the
fitness landscape enough to change the adaptive options
available to a solution’s offspring. For example, consider the
case where a solution stabilizes (converges in objective space).
If contextual sensitivity is weak, then changes to solution
interactions during fitness evaluation will not be able to change
this stability. On the other hand, if contextual sensitivity is
strong, changes in context may sometimes destabilize an
otherwise stable solution and allow for new adaptations to take
place. It is this second case that is frequently observed in
biological evolution and that would be interesting to observe
in MOO.
Previous studies have also investigated the relationship
between multi-objective optimization and coevolution [12]
[13] [8]. In [12], they describe how coevolution can be framed
as a multi-objective optimization problem where every
individual used to evaluate the fitness of another can be
thought of as a distinct objective for that individual. They go
on to argue that multi-objective optimization techniques and
concepts such as Pareto dominance can be directly applied to
coevolutionary systems which they later demonstrate in [13]
(but also see [14]). Furthermore, concepts such as Pareto
dominance have been found to be useful in guaranteeing
monotonic improvements in coevolutionary systems [15].
However, unlike these previous studies which have focused on
applying concepts from multi-objective optimization to
coevolution, this paper investigates whether coevolution is an
observable feature in standard MOEAs.
1.3 Outline
This study investigates whether population-based search
algorithms operating in an MOO environment can display
characteristics commonly attributed to coevolution. To test
this, it is necessary to design experimental conditions so that
the ONLY interaction between individuals in an evolutionary
algorithm is through fitness ranking. The next section
describes the main features of such an EA which is followed
by experimental results in Section 3. Section 4 discusses how
our results may be important to two competing theories of
evolution: Self-Organized Criticality and Dual Phase
Evolution. Conclusions are drawn in Section 5.
2 Experimental Setup
2.1 Species Model
Several experimental conditions must be observed in order to
investigate whether interaction-based fitness measurements
such as linear ranking can enable coevolutionary behavior in
an EA. The pseudocode for our algorithm highlights these
changes and is provided in Figure 3.
More intriguing information
1. Strategic Investment and Market Integration2. Globalization, Divergence and Stagnation
3. The name is absent
4. Shifting Identities and Blurring Boundaries: The Emergence of Third Space Professionals in UK Higher Education
5. The name is absent
6. The name is absent
7. Education and Development: The Issues and the Evidence
8. ROBUST CLASSIFICATION WITH CONTEXT-SENSITIVE FEATURES
9. Implementation of Rule Based Algorithm for Sandhi-Vicheda Of Compound Hindi Words
10. The name is absent