Evidence of coevolution in multi-objective evolutionary algorithms

Parent
Population

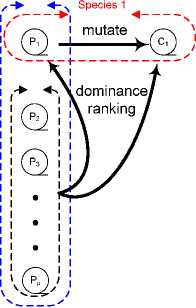
Figure 2: fitness evaluation and species adaptation in ESIM.

C1 replaces P1 if its ranking is higher and it is not dominated by
P1.

In these experiments, we use an Evolutionary Species Island
Model (ESIM) that captures two important features of natural
evolution: i) no interbreeding is allowed between species and
ii) a constrained set of species participate in defining the fitness
of others. In ESIM, each individual represents a distinct
species and the adaptation of species occurs through mutation.
Also, species only interact through fitness calculations, which
involves dominance ranking as defined in (1).

The ESIM does not allow direct competition between species
meaning that, although a species can adapt (through mutation),
no speciation or extinction events take place. Figure 2
illustrates these aspects of the algorithm. The removal of direct
competition between species was viewed as necessary to ensure
that the only interaction taking place was through definitions of
fitness and not through competitive selection. Also, allowing
for competitive selection introduces a branching process into
the (species) population dynamics which would make it more
difficult to determine the presence of coevolution in our
analysis.

Investigating Coevolution: Our study of coevolutionary
behavior involves changing the context for fitness evaluation
(described here) and analyzing whether this can influence the
evolution of species (described in Section 3.1). Changes in
context occur in the following manner. First, species are
grouped into islands where species within the island participate
in defining each other’s fitness. Migration events between
islands are then used as a tool for manually introducing
changes to who an individual species interacts with. Migration
takes place using a series of pair-wise swaps with the number
of swaps controlling the size of the migration event.

Migrations cause changes in which species interact during
ranking calculations (defined in (1)). Because each species
evolves through a localized sampling of genotype space (and
not through recombination or speciation), any changes to the
adaptive options of a species after a migration must be a result
of morphological changes to the species fitness landscape.
Hence, these migration events provide a well-controlled
change in context that can be used as a tool for investigating
the presence of coevolution.

Initialize EA into four equally sized islands

Evaluate each individual (in each island)

Determine Fitness of each individual using (1)

FOR each generation

FOR each parent in an island

Generate child Ci by mutating parent Pi

Evaluate Ci on test problem

Calculate Fitness F of Pi U (P- P₁)^t

Calculate Fitness F of Ci U (P- P₁)^t

FOR each parent in island

IF {F(C_i) > F(Pi)} ∧- {dom(Pi, Ci)} THEN
Ci replaces Pi

Store phenotypes of new population in archive

Calculate ΔPh over last τ generations using (2)
Every 300 generations, conduct a migration event
↑ Ranking takes place between individuals within the same island

Figure 3: Pseudocode for ESIM.

Remaining algorithm details: The total population size was
set to μ=64 with species divided into four equally sized islands
(i.e. islands with population size of 16). For each test problem
considered, the solution space was defined using real gene
encoding of dimensionality n. Offspring were copies of a
parent but with each gene mutated with a 2/n probability and
with mutations occurring by locally sampling alleles. Single
objective and multi-objective test problems used in these
experiments are listed in Table 1. Only two objectives are
considered (m=2) in MOP experiments. Unless stated
otherwise, results are averaged over 30 runs.

Table 1: Single and multiple objective test problems. More
information on parameter settings (second and fifth columns)
is available in the references provided.

<<   <   1   2   3   4   5   6   >   >>