IJCSI International Journal of Computer Science Issues, Vol. 4, No 1, 2009
19
The algorithm used in this research is based on the
mathematical manipulation of the probabilities of the top
100 most used keywords extracted from each web page.
However, the separate probabilities alone would not be
sufficient in classifying a new web page. The
classification of each page requires the combination of the
probabilities of all the separate features {f1, f2, ... fi, ..,
fn} into one probability, as in eq. 3 :
Л
arg max{P(Cn ∣ιv)} « - P(,Cn) ∏ P(f, ∣Cπ)
" ^ ɪ=- (3)
where z is a scaling factor dependent on the feature
variables, which helps to normalise the data. This scaling
factor was added as we found that when experimenting
with smaller datasets, the feature probabilities got very
small, which made the page probabilities get close to zero.
This made the system unusable.
Once the probabilities for each category have been
calculated, the probability values are compared to each
other. The category with the highest probability, and
within a predefined threshold value, is assigned to the web
page being classified. All the features extracted from this
page are also paired up with the resulting category and the
information in the database is updated to expand the
system’s knowledge.
Our research adds an additional step to the traditional NB
algorithm to handle situations when there is very little
evidence about the data, in particular during early stages
of the classification. This step calculates a Believed
Probability (Believed Prob), which helps to calculate more
gradual probability values for the data. An initial
probability is decided for features with little information
about them; in this research the probability value decided
is equal to the probability of the page, given no evidence
(P(Cn)) The calculation followed is as shown below:
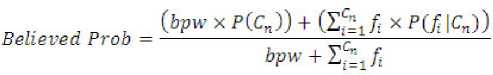
(4)
where: bpw is the believed probability weight (in this case
bpw = 1, which means that the Believed Probability is
weighed the same as one feature).
The above eliminates the assignment of extreme
probability values when little evidence exists; instead,
much more realistic probability values are achieved, which
has improved the overall accuracy of the classification
process as shown in the Results section.
4. Results
4.1 Performance Measures
The experiments in this research are evaluated using the
standard metrics of accuracy, precision, recall and f-
measure for Web Classification. These were calculated
using the predictive classification table, known as
Confusion Matrix (Table 1).
Table 1: Confusion Matrix
|
PREDICTED | |||
|
IRRELEVANT |
RELEVANT | ||
|
ACTUAL |
IRRELEVANT |
TN |
FP |
|
RELEVANT |
FN |
TP | |
Considering Table 1:
TN (True Negative) ÷ Number of correct predictions that
an instance is irrelevant
FP (False Positive) ÷ Number of incorrect predictions
that an instance is relevant
FN (False Negative) ÷ Number of incorrect predictions
that an instance is irrelevant
TP (True Positive) ÷ Number of correct predictions that
an instance is relevant
Accuracy - The proportion of the total number of
predictions that were correct:
Accuracy (%) =
(TN + TP) / (TN + FN + FP + TP) (5)
Precision - The proportion of the predicted relevant pages
that were correct:
Precision (%) = TP / (FP + TP) (6)
Recall - The proportion of the relevant pages that were
correctly identified
Recall (%) = TP / (FN + TP) (7)
F-Measure - Derives from precision and recall values:
F-Measure (%) =
(2 x Recall x Precision) / (Recall + Precision) (8)
The F-Measure was used, because despite Precision and
Recall being valid metrics in their own right, one can be
optimised at the expense of the other ([22]). The F-
Measure only produces a high result when Precision and
Recall are both balanced, thus this is very significant.
A Receiver Operating Characteristic (ROC) curve analysis
was also performed, as it shows the sensitivity (FN
classifications) and specificity (FP classifications) of a
IJCSI
More intriguing information
1. The demand for urban transport: An application of discrete choice model for Cadiz2. Workforce or Workfare?
3. Technological progress, organizational change and the size of the Human Resources Department
4. The name is absent
5. On the Integration of Digital Technologies into Mathematics Classrooms
6. Une nouvelle vision de l'économie (The knowledge society: a new approach of the economy)
7. Ein pragmatisierter Kalkul des naturlichen Schlieβens nebst Metatheorie
8. The name is absent
9. Valuing Farm Financial Information
10. The name is absent