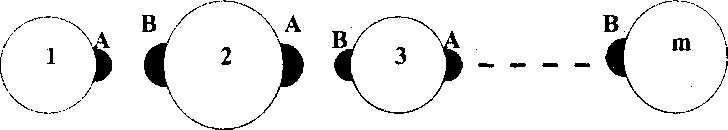
Figure 4.1: Schematic of the formation of a linear chain of m segments from m associating
spheres.
4.2.3 Equilibrium density profile
Substituting the free energy functional derivatives in Euler-Lagrange eqn. 4.2 for
a segment a gives
lnpα5(r) +
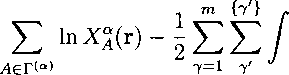
^AEX,hs ^AEX,att
+^ <5∕⅛es(r) + δpsaeg(r) ~ Va
nse9 / x b У contact [{Pα 9 (r 1 ) }] ,
^(ri)---⅛7W---
(4.22)
The set of these non-linear equations (for m segments) can be solved with eqn. 4.9 for
Хд, for the density profile of the segments. However, in eqn. 4.9, Хд for a segment
a depends on Xβ+1 for segment a + 1. This coupling of Хд and X⅛+1 leads to
numerical complexities. This interdependence is decoupled for a linear chain (of m
segments, see fig. 4.1) by simultaneously solving eqn. 4.22 for the segment densities
and eqn. 4.9 for the X%,s. The derivation is shown in the appendix. It should be
noted that the approach can be extended to branched chains, as shown in chapter 7.
The final expressions for Хд and X⅛ are given by
92
More intriguing information
1. Monetary Policy News and Exchange Rate Responses: Do Only Surprises Matter?2. The name is absent
3. How to do things without words: Infants, utterance-activity and distributed cognition.
4. Informal Labour and Credit Markets: A Survey.
5. The name is absent
6. Naïve Bayes vs. Decision Trees vs. Neural Networks in the Classification of Training Web Pages
7. The Complexity Era in Economics
8. The name is absent
9. The name is absent
10. Literary criticism as such can perhaps be called the art of rereading.