The name is absent

with grid size, ∆z = 0.1σ. The iteration starts with bulk densities for the density
profiles of all the segments. The D_js are then calculated using eqs. 4.25 followed by
the calculation for ∕_lj∙s and I2,jS using the recurrence relations. A set of new density
profiles is obtained from eqs. 4.31, which are then mixed with the previous results
as the new input. These steps are repeated until the converged density profile is
obtained. All the numerical integrations were performed using the trapezoidal rule.

4.3 Results and discussion

The density profile of a segment j, in a linear chain of m segments is given by

p_j(r_j) = ехр(врм) I-Idr₁-dr_j-₁dr_j+1..dr_mexp           - βV_l^ex‰)∖ j ɪɪ ∆<^v+υ(r_i,r_l+1).

J ■'                               ∖⅛=ι                       J _i=1

(4.33)

From eqn. 4.33, it follows that

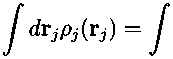
dr_j-1P_j-ι(r_j-1),

(4.34)

which means that modified iSAFT constrains the overall stoichiometry of the chain
even for complex heteronuclear systems. As a preliminary test to check the accuracy
of modified iSAFT, it was first applied to homonuclear hard chain fluids confined in
slit-like pores. The results are in good agreement with molecular simulation and are
similar to iSAFT [60]. Hence, they are not repeated in this work.

95

<<   104   105   106   107   108   109   110   >>

More intriguing information