energy contribution, Aεx∙hs due to volume exclusion∕short range repulsion, AEX'assoc
due to association, and AEX,att due to long range attraction. The ideal gas functional
is defined as
/m
⅛∑∕>rs(n)(∣n∕>Γ(n)-ι). (3.22)
α=l
Aεx'hs ɪɛ caιcuιated from Rosenfeld’s FMT [110] for mixtures of hard sphere fluids.
Aex,assoc can be written following TPTl (eq. 3.8) as
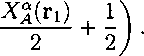
(3.23)
= Z drι∑pse9(rj £ (lnjɑ(ri)-
α=l A∈Γ<α) ʌ
The first summation is over all the segments a, and the second over all the association
sites on segment a. Хд denotes the fraction of segments of type a which are not
bonded at their site A. This fraction is given by the law of mass action.
*>ι) =
1
1 + ʃ ⅛2Xg'(r2)Δ-'(∏, r2)p7(r2) ’
(3.24)
where a' denotes the neighboring segment of a, site A on a bonds to site B on a',
and
∆αα'(rι,r2) = KFaa'(r1,r2)yaa∖r1,r2). (3.25)
K is a constant geometric factor which depends upon the bonding volume (the sites on
the segments are highly directional, they bond only when the sites on the two segments
are within specific orientations, see Segura et. al. [62]), yaa (rι,r2) is the cavity
75
More intriguing information
1. A Review of Kuhnian and Lakatosian “Explanations” in Economics2. The name is absent
3. 03-01 "Read My Lips: More New Tax Cuts - The Distributional Impacts of Repealing Dividend Taxation"
4. The name is absent
5. Learning and Endogenous Business Cycles in a Standard Growth Model
6. The name is absent
7. Innovation and business performance - a provisional multi-regional analysis
8. A dynamic approach to the tendency of industries to cluster
9. Permanent and Transitory Policy Shocks in an Empirical Macro Model with Asymmetric Information
10. Robust Econometrics