The name is absent

108

We take the SVD of this matrix, V = UΣX^τ, and choose a strong reduced system
size k_s < N_s. The POD matrix is then the first k_s columns of U, i.e. U = (7(:, 1 : fc_s).
Now we define the reduced variable by

v_s = Uv_s, v_s ∈ R^fes, U ∈ R,^jv≡×^fe≈_j

and then we substitute into (4.16) to obtain

∂t

Q I z_s 0
(c∕2)C H_s

oʃl ¹

Φ 2πα∆a?

⅞ι_w(t)^
. ш.

N(Uv_s(t), w_s(t))

Multiplying through by the projection matrices U and U^τ, we obtain the IRKA+P0D

reduced system
where the new “Hines” matrix is now completely dense, but of dimension (k_w + k_s) ×
( k_w 4^- k_s ).

∂t

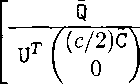
(Z_s 0) U ^
U⁷ H_sU

’ 0_l , ɪ ∣^BI_w(t)

U^τΦ] 27rα∆rr [u^τI_s(t)

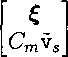
0
U^rN(Uv_s,w_s)

(4.17)

The final step is to reduce the nonlinear term, which follows the same procedure
as in §3.2.2. In this way we obtain a basis for the nonlinear term by taking snapshots
of N, and then using the DEIM to obtain the set of k_s spatial interpolation points z.

More intriguing information

1. Developments and Development Directions of Electronic Trade Platforms in US and European Agri-Food Markets: Impact on Sector Organization
2. The name is absent
3. ANTI-COMPETITIVE FINANCIAL CONTRACTING: THE DESIGN OF FINANCIAL CLAIMS.
4. Towards Teaching a Robot to Count Objects
5. Biologically inspired distributed machine cognition: a new formal approach to hyperparallel computation
6. Visual Perception of Humanoid Movement
7. Perfect Regular Equilibrium
8. Sectoral Energy- and Labour-Productivity Convergence
9. AN EXPLORATION OF THE NEED FOR AND COST OF SELECTED TRADE FACILITATION MEASURES IN ASIA AND THE PACIFIC IN THE CONTEXT OF THE WTO NEGOTIATIONS
10. The name is absent