106
and for convenience we define
N(vβ(f),ws(i)) ≡ (Φ(ws(t))e).(vs(t) + vs) - Φ(wβ(i))Ei (4.13)
which, along with (4.11), simplifies (4.9) to
∂t
Vw
Ww
Vw
Ww
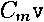
0
0
N(vs(⅛),ws(f))~
'0^
£
Φ
ɪ Γl∏w(t)^
2πα∆τ Is(t)
(4.14)
4.1.1 Model Reduction of the Weak Part
We focus first on reducing the weak part of the model by applying the linear
model reduction techniques of §2. In order to proceed with the model reduction we
need to write the weak part in the form of a standard linear system, but the coupling
term from Zs causes a problem. We make the assumption that this term can really
be treated as an input, i.e., we assume that vɪ is an input to the linear part, rather
than treating it as a state variable.
With this assumption on the inputs, let zw =
Ww
τ
be the state vector for
the weak part. Then the linear system whose observable is the voltage v^'w at the
weak compartment adjacent to the transition compartment is
z,(f) = Qz(i) + [B Zs]
(4.15)
v^(i) = Cz(t)
More intriguing information
1. Pursuit of Competitive Advantages for Entrepreneurship: Development of Enterprise as a Learning Organization. International and Russian Experience2. GENE EXPRESSION AND ITS DISCONTENTS Developmental disorders as dysfunctions of epigenetic cognition
3. The name is absent
4. EDUCATIONAL ACTIVITIES IN TENNESSEE ON WATER USE AND CONTROL - AGRICULTURAL PHASES
5. Temporary Work in Turbulent Times: The Swedish Experience
6. A Classical Probabilistic Computer Model of Consciousness
7. The name is absent
8. An Efficient Circulant MIMO Equalizer for CDMA Downlink: Algorithm and VLSI Architecture
9. Palvelujen vienti ja kansainvälistyminen
10. The Making of Cultural Policy: A European Perspective