19
Eigenvalues of A for standard Hodgkin-Huxley kinetics
0.4r ×
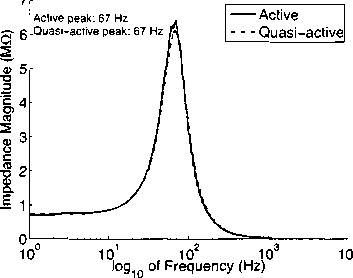
Frequency response of isopotential HH cell
0.3
0.2
0.1
∈ 0 × ×
-0.1
-0.2
-0.3
—0.4-------------'--------------'--------------'-------------'----------x
-5 -4 -3 -2 -1 0
Reλ
Figure 2.4: Left: Eigenvalues of the 4-by-4 matrix A given in (2.13). Right: Frequency
response of the active (solid) and quasi-active (dashed) models using standard HH kinetics.
evaluated numerically via a high-order quadrature scheme such as Clcnshaw-Curtis
quadrature, as described in (Trefethen, 2007).
Not only does the eigenvalue decomposition yield an analytic solution, but also the
eigenvalues of A will tell us whether resonant frequencies exist and, if so, where in the
spectrum to look for them. Recall that if A is an eigenvalue of A and if Imag(A) ≠ 0,
then the resonant frequency is in the neighborhood of
2πlmag(λ)
Cl7t∙ — ` .
1000
where the 1000 in the denominator is to convert from milliseconds to seconds (i.e.,
from mHz to Hz). If Real(A) — 0 then ωr is exactly the resonant frequency. However,
the quasi-active system is dissipative, meaning that it is possible that some eigenvalues
have Real(A) ≠ 0, and thus the above equation is only an approximation to ωr.
More intriguing information
1. National urban policy responses in the European Union: Towards a European urban policy?2. Ronald Patterson, Violinist; Brooks Smith, Pianist
3. The name is absent
4. TWENTY-FIVE YEARS OF RESEARCH ON WOMEN FARMERS IN AFRICA: LESSONS AND IMPLICATIONS FOR AGRICULTURAL RESEARCH INSTITUTIONS; WITH AN ANNOTATED BIBLIOGRAPHY
5. The name is absent
6. Education Research Gender, Education and Development - A Partially Annotated and Selective Bibliography
7. Agricultural Policy as a Social Engineering Tool
8. News Not Noise: Socially Aware Information Filtering
9. The name is absent
10. ISO 9000 -- A MARKETING TOOL FOR U.S. AGRIBUSINESS