25
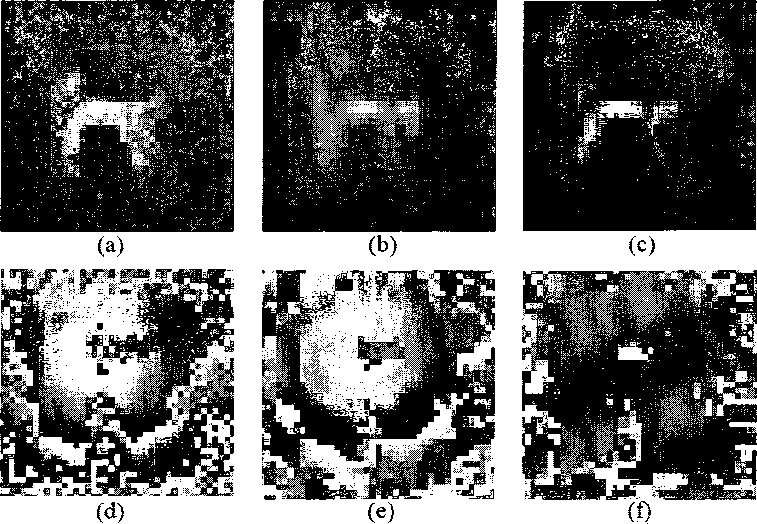
Figure 3.2 : Compressed sensing imaging results, (a) Magnitude of image recon-
structed by inverse Fourier transform using the full data set (4096 uniformly sampled
measurements), and (d) its phase. Note the phase distortion inherent in the THz beam
in (d). Compressed sensing reconstruction result using 500 measurements (12%) from
the full data set: (b) magnitude, and (e) phase. Compressed sensing with phase cor-
rection improves image quality and eliminates phase distortion (see (c) and (f)). All
figures show a zoom-in view on a 40 × 40 grid centered on the object.
and the measurement matrix Φ is M × N. Despite using fewer measurements, CS
can achieve perfect reconstruction of the object, assuming its sparsity, through an
optimization procedure [8]. Many optimization algorithms exist to solve this inverse
imaging problem. These algorithms aim to solve the minimization problem:
argmin ∣∣rr∣∣1 subject to constraint y = Фж, (3.1)
where ∣∣rr∣∣ι denotes the /!-norm [8]. Sometimes, when the original image x is
More intriguing information
1. RETAIL SALES: DO THEY MEAN REDUCED EXPENDITURES? GERMAN GROCERY EVIDENCE2. FUTURE TRADE RESEARCH AREAS THAT MATTER TO DEVELOPING COUNTRY POLICYMAKERS
3. Ongoing Emergence: A Core Concept in Epigenetic Robotics
4. The open method of co-ordination: Some remarks regarding old-age security within an enlarged European Union
5. An Empirical Analysis of the Curvature Factor of the Term Structure of Interest Rates
6. Magnetic Resonance Imaging in patients with ICDs and Pacemakers
7. On the Desirability of Taxing Charitable Contributions
8. Tobacco and Alcohol: Complements or Substitutes? - A Statistical Guinea Pig Approach
9. Forecasting Financial Crises and Contagion in Asia using Dynamic Factor Analysis
10. Who’s afraid of critical race theory in education? a reply to Mike Cole’s ‘The color-line and the class struggle’