The name is absent

65

(b) Given K and φ, generate a new set of parameters (β*,δ*) from the distributions

p(∕3⅛ I N, φ, K) — Ga I β_k Sβ +    М2, ^sβtβ + ^ⁱ

ies_k

and

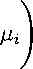
for к = 1,..., K.

(d) Update the total mass parameter a:

(1) let a denote the currently imputed parameter value. Generate η ~ Beta(a+
l,n) and,

(2) sample the new value of a from

p(a I K, η) =π_ηGa(a ∖a_a + K,b_a- log η)

+(1 - 7Γη)Gα(α ∣ a_a + K - l,ftɑ - Iogr?),

where,

7Γη        ɑɑ ∣^- ɪ

1 - π₄   n(b_a - log 77)

(e) Update hyperparameters of G₀- Simulate from the complete conditional posterior
distributions,

p(tβ I M β↑-, ∙ ∙ ∙, β*κ) — Ga I tβ a_tg + Ksp, b_tfj + Sβ fik i ■

⅛=ι

.., δ*_κ) = Ga t<₅ a_ts + Ks_δ, b_ts + s_δ∑δ*_k

fc=l

(f) Finally, update μ_i and the hyperparameter t_μ:

p(μ∙i I N, t_μ,βi, δβ — Ga{μ_i ∣ Nn + Na +    + s_μ, 1 + ∕¾ + δi + s_μt_μ}.

p(t_μ ∖ μ₁,...,μ_n) = Ga I t_μ a_tμ + ns_μ,

In order to avoid the chain to get “trapped” we reinitialize the configuration every
10,000 Gibbs sampling iterations with K — n getting new values for (∕3J, jɪ ),..., (∕3*, J*)
by resampling from (3.4.2) without changing the values of the remaining parameters.

<<   74   75   76   77   78   79   80   >>

More intriguing information