90
time with the current input to yield the solution to a space and time-dependent input. These
Greens functions are identical to the concept of an impulse response from engineering.
5.4.2 Cable equation in two dimensions
While the one-dimensional cable equation is useful for computing the response of the rod
network to a bar stimulus, where current flow is restricted to the dimension perpendicular
to the bar (see figure 5.1), to understand how coupling in the rod network reduces noise in
photoreceptors, the entire network must be considered.
The cable equation has been studied extensively for one-dimensional problems relating
to the voltage distribution in a neuron, but a two-dimensional electrical cable is a much less
common topology. One example of a two-dimensional cable an the array of rod photore-
ceptors connected to one another in a grid, as shown in figures 4.3 and 5.8.
The steady-state response for a current i injected into a continuous two-dimensional
cable is:
τz∕ ʌ .Rcv (r∖
(5.7)
(5.8)
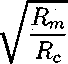
Where K is a modified Bessel function of the second kind with a = 0 [69]. The solution
is radially symmetric, so r = y∕x2 + y2.
More intriguing information
1. Strategic monetary policy in a monetary union with non-atomistic wage setters2. Smith and Rawls Share a Room
3. Technological progress, organizational change and the size of the Human Resources Department
4. Segmentación en la era de la globalización: ¿Cómo encontrar un segmento nuevo de mercado?
5. The name is absent
6. Database Search Strategies for Proteomic Data Sets Generated by Electron Capture Dissociation Mass Spectrometry
7. The name is absent
8. The name is absent
9. TOMOGRAPHIC IMAGE RECONSTRUCTION OF FAN-BEAM PROJECTIONS WITH EQUIDISTANT DETECTORS USING PARTIALLY CONNECTED NEURAL NETWORKS
10. Aktive Klienten - Aktive Politik? (Wie) Läßt sich dauerhafte Unabhängigkeit von Sozialhilfe erreichen? Ein Literaturbericht