The name is absent

11

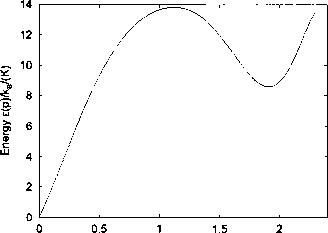
Momentum p∕Fι∕(A¹)

Figure 2.2: (Color online) Dispersion curve for elementary excitations in liquid helium, adapted

from reference [6]. The roton region is near the minimum.

2.2.2 A numerical example

As an example, we use the numerical scheme discussed above to seek the ground state for
a two-dimensional dipolar condensate in an infinite well, i.e. the hard-wall boundary con-
dition we use in the calculation. The original motivation for this calculation is originated
from our interests in the roton instability in dipolar condensate [8]. A roton is an excitation
or quasiparticle, which was first found in superfluid ⁱHe due to its peculiar dispersion as
shown in the Fig. 2.2, which may lead to the instability of the system and hence induce a
charge density-wave state. It has been reported that such roton minimum also exists in the
excitation spectrum of a dipolar condensate [7, 8]. Therefore, we expect that the density-
wave states would be an energetically favorable metastable state near this roton minimum
area before the condensate goes to collapse.

As shown in Fig. 2.3, the density wave structures are observed to appear near the bound-
aries. However, away from the boundary, the density waves are quickly damped. With

<<   17   18   19   20   21   22   23   >>

More intriguing information