Rectilinear Drawing
61
faarg(r sin ψ)dψ==O
Thus we infer that the integral last written vanishes identi-
cally in r. Now introduce the variable s=r sin ψ in this
integral. In this way we conclude that we must have
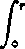
g(ʃ)^ʃ
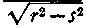
= 0.
This is a special case of a type of integral equation treated
by Abel to which we shall refer later. Let us solve it ex-
plicitly by his simple, direct method, of which the gen-
eralization is immediate. Multiply this integral through by
r∕V'p2-τ2 where ʃ <r <p, and integrate as to r from 0 to p.
We obtain thus
dr = 0.
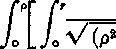
rg(ʃ)^ʃ
-r2)(r≡-J2)
Making a valid interchange of the order of integration (see
fig. 6) this becomes
fp / ∕,p rdr ∖
J0 gt's∖js √(p2-r2) (r2-J2)Λ≡0
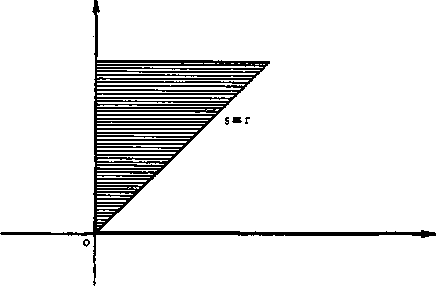
Fig. 6
More intriguing information
1. THE UNCERTAIN FUTURE OF THE MEXICAN MARKET FOR U.S. COTTON: IMPACT OF THE ELIMINATION OF TEXTILE AND CLOTHING QUOTAS2. The name is absent
3. The name is absent
4. EMU: some unanswered questions
5. Spatial Aggregation and Weather Risk Management
6. Integration, Regional Specialization and Growth Differentials in EU Acceding Countries: Evidence from Hungary
7. Urban Green Space Policies: Performance and Success Conditions in European Cities
8. The Role of Land Retirement Programs for Management of Water Resources
9. Rent Dissipation in Chartered Recreational Fishing: Inside the Black Box
10. Categorial Grammar and Discourse