Rectilinear Drawing 63
⅛ r F if) dr
admits a continuous derivative, in which case we have necessarily
n∖ f(Λ 1 d [3rp^dr
as the unique solution.
If we do not wish to restrict attention to continuous func-
tions F and f, various extensions are clearly possible. One
of the simplest of these would be that in which F is taken
integrable in the sense of Lebesgue over the given region,
while / is similarly integrable. Here we should be led to
require that the integral /(ʃ) not only exist but be absolutely
continuous.
5∙ A SPECIAL SYMMETRIC CASE
We shall apply the preceding formal work to the discussion
of a particular symmetric case which is especially interesting,
namely,
F(r)
0 for r<r0
∖k forr>√
Here the function F(f) is discontinuous at r = r0 but not in a
way such as to cause essential difficulty. In fact if we apply
the formula (2) to this case we find at once
∕ω= ±
l2ιr
' 0 for ʃ <r0
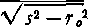
for s>ra.
Since the function /(ʃ) so obtained is everywhere positive
and leads to no difficulty in (1), we conclude that it is pos-
sible to set up a symmetrical distribution of lines outside of
the circle s = r0 in such wise that the region outside of the
given circle is of a uniform gray.