KETONEN et al. : PERFORMANCE-COMPLEXITY COMPARISON OF RECEIVERS FOR A LTE MIMO-OFDM SYSTEM
3361
been reported in the literature. Application-specific integrated
circuit (ASIC) implementation of a soft output AT-best sphere
decoding algorithm has been presented in [12], a fixed sphere
decoder in [15] and optimizations of a hard-output Λ'-best in
[16]. An application-specific instruction set processor (ASIP)
has been designed for a 2 × 2 64-QAM system A-best LSD
with transport triggered architecture (TTA) in [17]. An FPGA
implementation of a hard output breadth-first sphere detector
can be found in [18]. ASIC implementations of depth-first and
K-best sphere decoding algorithms have been presented in [19].
We compared the SIC and A’-best LSD implementations for
a field-programmable gate array (FPGA) in [20]. The receivers
were designed for 2 × 2 4-QAM, 16-QAM, and 64-QAM and
implemented with the Xilinx System Generator. The SIC re-
ceiver was found to be slightly more complex than the A^-best
LSD receiver, but the latency of the SIC receiver was lower with
all modulations. However, a complete analysis of the achiev-
able communication performance and required implementation
complexity with various detectors in the evolving LTE standard
has received very little if any attention in the open literature.
In this paper, we analyze the performance-complexity
tradeoff of various soft-output MIMO detectors in the LTE
system downlink context. More specifically, the perfor-
mances, implementation complexities and latencies of the plain
LMMSE, the LMMSE based SIC receiver and the A’-best LSD
receiver are studied and compared to each other; a modification
to the tree search of the AT-best LSD is also introduced to
simplify its implementation. FPGA and ASIC implementation
results are presented for 2 × 2 and 4×4 MIMO configurations
with QPSK, 16-QAM, and 64-QAM. Their communication
system performances are compared via computer simulations
with LTE parameters [21] and realistic channel models. The
latency of the entire receiver is considered and the iterative
(turbo) versions of the SIC and A?-best LSD are compared to
the noniterative LMMSE and A’-best LSD receivers.
The results provide a solid basis for systematic complexity-per-
formance tradeoff of different detection algorithms for applica-
tion in the evolving next generation cellular access standard. The
communication system performance is characterized by frame
error rate (FER), which is usually transformed to data transmis-
sion throughput. The transmission throughput is defined to be
equal to the nominal information transmission rate of informa-
tion bits times (1 - FER). In other words, the throughput mea-
sure characterizes the rate and the reliability. The implementa-
tion complexity is characterized as the numbers of FPGA slices,
18-kbit blocks of random access memory (BRAM) and dedicated
digital signal processor (DSP) slices as well as equivalent gates.
The latency of the implementation is also analyzed, and reflected
as detection rate of a particular implementation. The detection
rate refers to the nominal rate by which the algorithm can make
data decisions, but it differs from the transmission throughput in
the sense that it tells nothing about the reliability of the decisions.
The measure which combines both the hardware limitations and
the reliability is called goodput, i.e., the minimum of the trans-
mission throughput and hardware detection rate of information
bits.
The paper is organized as follows. The system model is pre-
sented in Section II-A. The K-best LSD algorithm is introduced
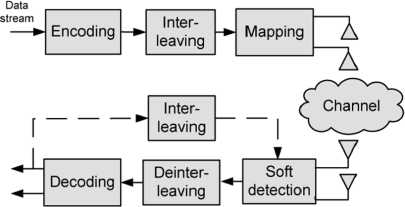
Fig. 1. The MIMO-OFDM system model.
in Section II-B. The SIC algorithm is introduced in Section II-C.
Some performance examples are presented in Section III. The
complexities and latencies are compared in Section IV. Discus-
sion and conclusions are presented in Sections V and VI.
II. Receiver Algorithms
A. System Model
An OFDM based MIMO transmission system with N
transmit (TX) and M receive (RX) antennas, where N < ΛT, is
considered in this paper. A layered space-time architecture with
horizontal encoding is applied. The cyclic prefix of an OFDM
symbol is assumed to be long enough to eliminate intersymbol
interference. The system model is illustrated in Fig. 1. The
received signal can be described with the equation
y; -!T.x,. ■ /∕λ. p = 1,2,...,P (1)
where P is the number of subcarriers, xp ∈ Cλ' is the trans-
mitted signal on pth subcarrier, ηp ∈ Cm is a vector containing
identically distributed complex Gaussian noise with variance
σ2 and Hf, ∈ Cm хЛ is the channel matrix containing com-
plex Gaussian fading coefficients. Bit-interleaved coded mod-
ulation (BICM) is applied. The entries of xp are drawn from
a complex QAM constellation Ω and ∣Ω∣ = 2$, where Q is
the number of bits per symbol. The set of possible transmitted
symbol vectors is Ωλ∖ The binary vector bj, corresponding to
Xp has elements bλ, where λ = (k — 1)Q,..., ⅛Q — 1 with the
⅛th element of xj,.
B. The K-Best LSD Algorithm
The ML detection method minimizes the average error prob-
ability and it is the optimal method for finding the closest lattice
point. The ML detector calculates the Euclidean distances (EDs)
between the received signal vector у and lattice points Hx, and
returns the vector x with the smallest distance, i.e., it minimizes
xml - arg min ∣∣y - Hx∣∣2. (2)
The SD algorithms solve the ML solution with a reduced
number of considered candidate symbol vectors. They take into
account only the lattice points that are inside a sphere of a given
radius. The condition that the lattice point lies inside the sphere
can be written as
∣∣y - Hx∣∣2 ≤ C,o. (3)