An Efficient Circulant MIMO Equalizer for CDMA Downlink: Algorithm and VLSI Architecture

Yuanbin Guo et al.

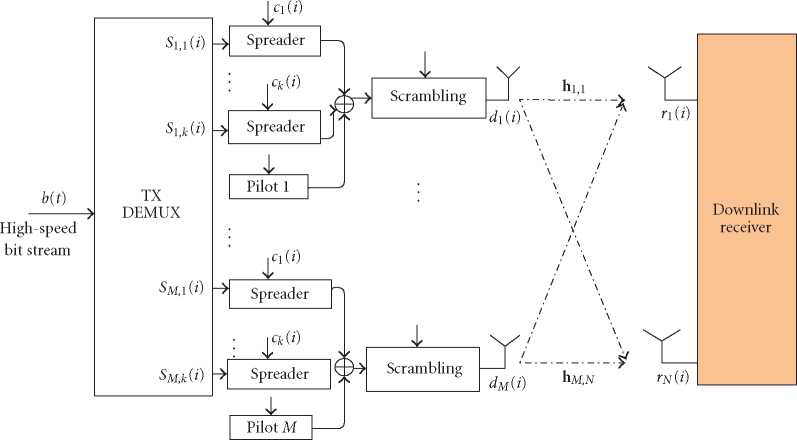
Figure 1: The system model of the MIMO multicode CDMA downlink.

chip from all the N Rx antennas, we form a signal vector as
rA = [r(i+F)^T, ...,r(i)^T,...,r(i-F)^T]^T.Here,F is the obser-
vation window length corresponding to the channel length.
In the vector form, the received signal can be given by

M

rA(i) =     Hmdm(i),                  (2)

m=1

where Hm is a block Toeplitz matrix constructed from the
channel coefficients as shown in [20]. The multiple receive
antennas’ channel vector is defined as hm (l) = [hm,1 (l),
..., hm,n(l), ..., hm,N (l)]^T. The transmitted chip vector for
the mth transmit antenna is given by dm(i) = [dm(i +
F),...,dm(i),...,dm(i-F-L)]^T.

3. LMMSE TAP SOLVER WITH CIRCULANT
APPROXIMATION

3.1. LMMSE chip equalizer

LMMSE chip-level equalization has been one of the most
promising receivers in the single-user CDMA downlink.
Chip equalizer estimates the transmitted chip samples by a
set of linear FIR filter coefficients wH(i) to restore the code
orthogonality as

^           . TT

d m ( i ) = WH ( i )rA ( i ).

It is well known that the LMMSE chip equalizer coefficients
are given by minimizing the MSE between the transmitted
and recovered chip samples as

where σj(i) is the transmitted chip power. R_rr(i) and h_m(i)
are the covariance estimation and channel estimation, re-
spectively. Here, the covariance matrix is estimated by the
time-average with ergodicity assumption as

1 NB -1

Rrr(i) = E ^[rA(i)rH(i)] = — ɪ rA(i)rH(i),     (5)

N^B i=0

where NB is the length for the time average. The channel co-
efficients are estimated as hm(i) = E[rA(i)d^H_m(i)] using the
pilot symbols. In the HSDPA standard, about 10% of the to-
tal transmit power is dedicated to the common pilot chan-
nel (CPICH). This will provide accurate channel estimation.
By assuming that the channel is stationary over the observa-
tion window length, we can have a block-based operation by
omitting the chip index in R_rr(i), h_m(i), and w_m(i).

3.2. FFT-based circulant approximation tap solver

Using the stationarity of the channel and the convolution
property, it is easy to show that the covariance matrix is a
banded block Toeplitz matrix as

wm^pt(i) = argminE ∣^∣∣dm(i) - wH(i)ra(i)∣∣²1

Wm ( i )                                            (4)

= σd2( i )R rr ( i )^{- 1}h m ( i ),

where E[l] is an (N × N) block matrix with the cross-
antenna covariance coefficients. The dimension of the ma-
trix is (NLF × NLF ), where LF is determined by the channel
length L. In an outdoor environment, LF could be up to 32.

<<   1   2   3   4   5   6   >>

More intriguing information