EURASIP Journal on Applied Signal Processing
Stage 1
Stage 2
Stage 3
Stage 4
x(0) = 0
x(8) = 0
x(4)
x(12) = 0
x(2)
x(10) = 0
x(6) = 0
x(14) = 0
x(1)
x(9) = 0
x(5) = 0
x(13) = 0
x(3)
x(11) = 0
x(7) = 0
x(15) = 0
x
x
x
x
x
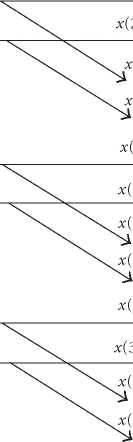
Figure 3: Reduced-state FFT butterfly tree.
Wι06∕Λ λ.>∙∕AΛΛ
> .∩, ' >. V < у ∕v '∙v >
1
W 6, А л Λ∕'.A.'∖ √
> / >
Wг i I W À Y \ \
ʌ W16'∙∕ΛV√'.
W136
÷-O∕τ
w 4б//
÷-CUΛ
W 15б/ /
W 6б/ /
÷-0-'-A
W 7б-'
÷-Oi-∙
-γ-∙->
unit, each operation involves a full complex multiplication,
which has 4 real multiplications and г real additions. Since
the kth subcarrier of the Fmm vector is
fmm (k) = emm (0)+2%
(Σ
i=1
emm(i)WL-Fki ,
Table 1: Complexity comparison for different FFT schemes.
(13)
|
Real mult |
Real add | |
|
Full FFT |
2Lp log2 Lp |
Lplog2 Lp |
|
RS-FFT w/o ZP |
2N log2 Lp - 2Lp + 2 |
Lp log2 Lp - 2Lp +2 |
|
RS-FFT with ZP |
2Lp log2 Lp - 6Lp + 12 |
Lp log2 Lp - 4Lp + 12 |
by defining the input sequence to the FFT module as {x(i)} =
[0, emm(1),..., em,m(L), 0, ..., 0], we only need to compute
the real part FFT of the x(i) to get fmm(k). From the but-
terfly decomposition, we have the recursion for the real-part
FFT computation as
% ( X ( к )) = % ( X 1( к )) + % ( WkpX2( к )),
%{X{к + L2p)) =%(X 1(к)) -%(WkpX2(к))
(14)
for к = 0, 1, ...,Lp/2 - 1. This reduces the complex multi-
plication and addition to only real multiplication and addi-
tion for one stage. The butterfly unit becomes a reduced-state
partial-butterfly-unit (PBFU) as the dotted line units shown
in Figure 3 for an example of 16-point FFT.
From the recursion, it can be shown that we can prune
the redundant computations by replacing the complex mul-
tiplication in the butterfly units for some portion of the FFT
BFU tree. Before considering the many zeros in the input
coefficients, the total number of PBFU is Lp - 1. Since the
total number of BFU is (Lp/2) log2 Lp, the total number of
full-BFU (FBFU) is given by (Lp/2) log2 Lp - Lp + 1. Con-
sidering that x(i) = 0onlyfori ∈ [1, L], L<Lp/2, we can
further truncate the computations related to the zero values.
After pruning all the unnecessary BFU branches, the FBFUs
and PBFUs only take effects from stage 3. The number of
FBFU is reduced to (Lp/2) * log2 Lp - 2Lp + 6. This also
reduces the number of memory access and register files for
stage 1 and stage 2 as well as in the partial BFUs. The fi-
nal data flow is shown as the BFU tree in Figure 3. In the
figure, only the shaded portion has full-BFUs. Table 1 sum-
marizes the required operations in terms of the real mul-
tiplications/additions and memory read/write. In the table,
RS-FFT indicates the reduced-state FFT- and ZP-means zero
pruning. Although the saving diminishes when the length of
FFT increases to a very large number, the RS-FFT with ZP
More intriguing information
1. The name is absent2. What should educational research do, and how should it do it? A response to “Will a clinical approach make educational research more relevant to practice” by Jacquelien Bulterman-Bos
3. The name is absent
4. Improvements in medical care and technology and reductions in traffic-related fatalities in Great Britain
5. LOCAL PROGRAMS AND ACTIVITIES TO HELP FARM PEOPLE ADJUST
6. The name is absent
7. The name is absent
8. Proceedings from the ECFIN Workshop "The budgetary implications of structural reforms" - Brussels, 2 December 2005
9. Dual Inflation Under the Currency Board: The Challenges of Bulgarian EU Accession
10. ROBUST CLASSIFICATION WITH CONTEXT-SENSITIVE FEATURES