An Efficient Circulant MIMO Equalizer for CDMA Downlink: Algorithm and VLSI Architecture

EURASIP Journal on Applied Signal Processing

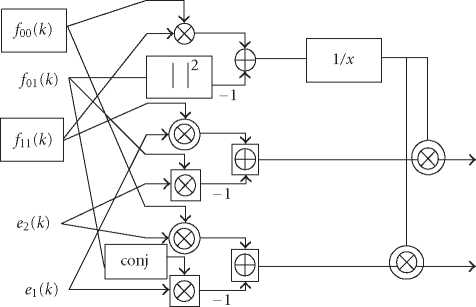
Figure 4: The merged 2 × 2 inverse and multiplication.

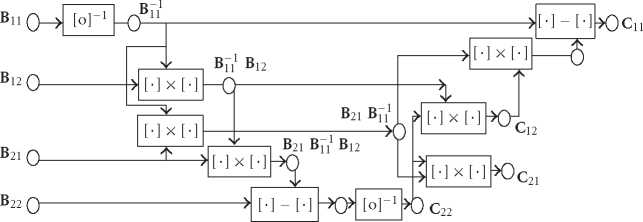
Figure 5: The data path of the partitioned 4 × 4 matrix inverse for each subcarrier.

It can be shown that the subblocks are given by the following
equations from the matrix inverse lemma [22]:

C22(i) = [B22(i) ^ B21(i)B11(i) ¹B12(i)]   ,

C12(i) = -B11(i)^-1B12(i)C22(i),

C21(i) = -C22(i)B21(i)B11(i)^-1,

C11(i) = B11(i)^-1 - C12(i)B21(i)B11(i)^-1.

Without looking into the data dependency, a straightfor-
ward computation will have 8 complex matrix multiplica-
tions, 2 complex matrix inverses, and 2 complex matrix sub-
tractions, all of the size (2 × 2). By examining the data de-
pendency, we will find some duplicate operations in the data
path. For a general case before considering the Hermitian
structure of the F[i] matrix, a sequential computation has the
data-dependency path given by Figure 5. The raw complex-
ity is given by 6 matrix mult, 2 inverses, and 2 substractions.
From the data path flow, the critical path can be identified.

Now we utilize the Hermitian feature of the F matrix
to derive more parallel computing architecture. Because the
inverse of a Hermitian matrix is Hermitian, that is, F^-1 =
[F^-1]^H, it can be shown that

B-1¹(i) = [B-¹(i)]H =⇒ C11(i) = [C11(i)]H,
B12(i) = [B21(i)]H =⇒ C12(i) = [C21(i)]H,     (22)

B22(i) = [B22(i)]H =⇒ C22(i) = [C22(i)]H.

This leads to the data path by removing the duplicate compu-
tation blocks that has the Hermitian relationship. However,
this straightforward treatment still does not lead to the most
efficient computing architecture. The data path is still con-
structed with a very long dependency path. To fully extract
the commonality and regulate the design blocks in VLSI, we
define the following special operators on the (2 × 2) matrices
for the different complex operations. These special operators
are mapped to VLSI processing units to deal with the special
Hermitian matrix.

Definition 1 (pseudo-power). pPow(a, b) = %(a) ■ %(b) +
3 ( a) ■ 3 ( b) is defined as the pseudo-power function of two
complex numbers and %(a, b) = %(a) ■ %( b) - 3 ( a) ■ 3 ( b)
is defined as the real part ofa complex multiplication.

Definition 2 (complex-hermitian-mult). For a general (2 ×2)
matrix A and a Hermitian (2 × 2) matrix B = B^H, we define
the operator CHM (Complex-Hermitian-mult) as

M(A, B) = AB = (a¹¹ a ¹²Wb¹¹ b²¹ ʌ .     (23)

a21 a22    b21 b22

Note that all the numbers are complex except {b11, b22} ∈ R.

Definition 3 (Hermitian inverse). For a (2 × 2) Hermitian
matrix B = B^H, the Hermitian inverse (HInv) operator is

<<   5   6   7   8   9   10   11   >>

More intriguing information