An Efficient Circulant MIMO Equalizer for CDMA Downlink: Algorithm and VLSI Architecture

EURASIP Journal on Applied Signal Processing

b11(r) b21 (r/i) b22(r)

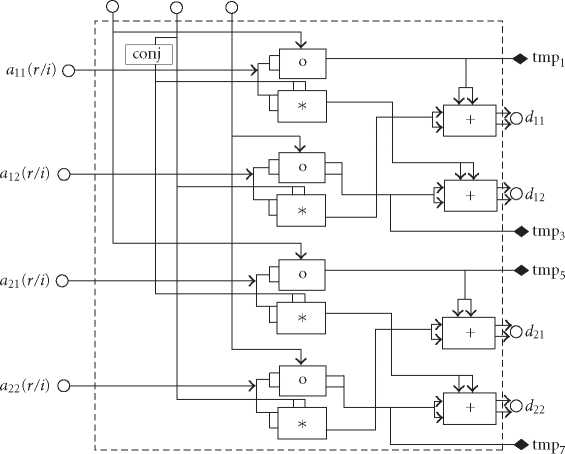
Figure 6: The simplified parallel VLSI RTL layout of the M(A, B) processing unit.

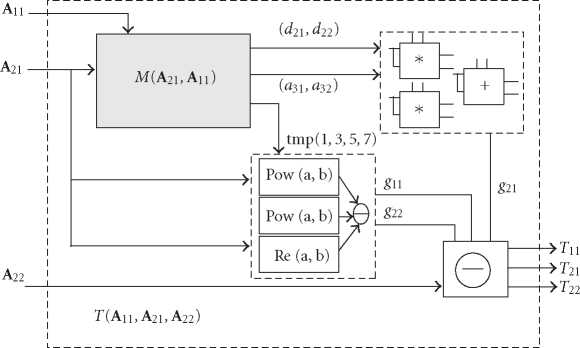
Figure 7: The VLSI RTL architecture layout of the T(A11,A21,A22) block.

transform T(A11,A21,A22)ofthe(4× 4) Hermitian matrix is
given by Figure 7. The output ports of the T(A11, A21, A22)
include the independent elements {t11, t21, t22}.

We can further simplify the top-level RTL schematic by
extracting the commonality of the M and T module designs
as in Figure 8 to eliminate the extra individual M module.
Thus, the results of C11, C12, and C21 are generated together
from the second T module. Compared with the design in
Figure 5, the architecture demonstrates better parallelism
and reduced redundancy. The data path is much better bal-
anced and facilitates the pipelining in multiple subcarriers
for high-speed design.

If we use a standard computing architecture of the par-
titioned (4 × 4) matrix inverse, we need 308 real multi-
plications before dependency optimization (DO). With a

straightforward DO, the complexity is still 244 real multipli-
cations. Traditionally, a complex multiplication is given by
“c = c_r + jc_i = (a_r + ja_i) * (b_r + jb_i) = (a_rb_r - a_ib_i)+ j(a_rbi +
ai br).” This has 4 real multiplications (RM) and 2 real ad-
ditions (RA). By rearranging the computation order, we can
reduce the number of real multiplications as (1) p1 = arbr,
p2 = aibi, s1  = ar + ai, s2 = br + bi; (2) cr = p1 - p2,

d = (p1 + p2), s = s1s2; (3) ci = s - d. This requires 3
real multiplications and 5 real additions in three steps. A sin-
gle T transform needs only 38 RMs for a (4 × 4) Hermitian
matrix. Thus, there are 90 RMs to compute the F(i)^-1 with
the optimized Hermitian architecture. This is only less than
1/3 of the real multiplications for a traditional architecture as
shown in Table 2. Note that the critical data path is also dra-
matically shortened with better modularity and pipelining.

<<   7   8   9   10   11   12   13   >>

More intriguing information