Yuanbin Guo et al.
11
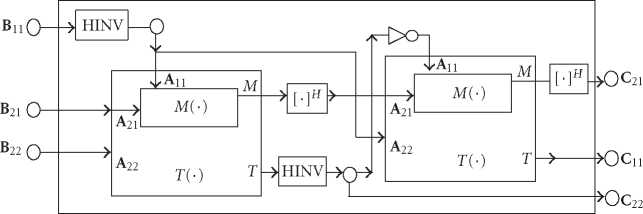
Figure 8: The commonality extracted VLSI design architecture based on T, M, and HINV.
5. COMPARATIVE PERFORMANCE AND
COMPLEXITY ANALYSIS
5.1. BER performance
The performance is evaluated in a MIMO-HSDPA simula-
tion chain for different antenna configurations. We compare
the performance of four different schemes: the LMS adap-
tive algorithm, the CG algorithm, the FFT-based algorithm,
and the DMI using Cholesky decomposition. We simulated
the Pedestrian-A and Pedestrian-B channels following the
I-METRA channel model [23], which are typical for high-
speed downlink application. The chip rate for the transmit
signal is 3.84 Mcps, which is in compliance with the 3GPP
standard. The channel state information is estimated from
the CPICH at the receiver. Ten percent of the total transmit
power is dedicated to the pilot training symbols.
We provide the simulation results for QPSK modula-
tion with antenna configuration in the form of (M × N).
In the figures, Lh is the channel delay spread. Figures 9
and 10 show the fully loaded system for Pedestrian-A and
Pedestrian-B channels with (2 × 2) configuration, while
Figure 11 shows a highly loaded system with 10 codes for
(2 × 2) Pedestrian-B channel. Figure 12 shows the simulation
results for Pedestrian-A with (4 × 4) configuration. It can be
seen that for Figure 9, the FFT-based algorithm overlaps with
both the DMI and the CG at 5 iterations very closely. In a
(2 × 2) case for Pedestrian-B channel, both the CG and FFT-
based algorithms show very small divergence from the DMI
at the very high SNR range in Figure 10. For a fully loaded
system, CG with 5 iterations seems to be slightly better than
FFT-based algorithm. But in a case with 10 codes, FFT-based
algorithm outperforms the CG for both 3 iterations and 5
iterations. In the (4 × 4) case as shown in Figure 12, the
FFT-based algorithm also outperforms the CG with 5 iter-
ations. However, because the realistic system is most unlikely
to work in the very high SNR range, the small difference in
the BER performance is negligible. In all cases, the DMI, CG,
and FFT-based algorithms significantly outperform the LMS
adaptive algorithm.
It should be pointed out that the performance of the
LMMSE-based chip equalizer is limited for the fast fading
channel because of its block-based feature could not track the
fast fading channel environments very well. To deal with this,
Table 2: Complexity reduction for submatrix inverse in F-1
Architecture RM
Traditional w/o DO(4 × 4) 308LF
Traditional w/ DO(4 × 4) 244LF
Hermitian opt(4 × 4) 90LF
a Kalman filter-based equalizer has been proposed in one of
the authors’ papers [24] with much higher complexity. The
discussion of the related architecture is out of the scope of
this paper.
5.2. Complexity
The complexity is a very important consideration for real-
time implementation. Although the complete equalizer sys-
tem consists of the correlation/channel estimation, the tap
solver, and the FIR filtering, we focus on the three-tap-solver
complexity with similar performance, that is, the DMI, the
CG, and the FFT-based algorithm. The other two parts are
common for the algorithms presented here. Cholesky de-
composition is assumed for the DMI. The complexity is com-
pared in terms of number of equivalent complex multiplica-
tions and additions.
For the DMI, the complexity is at the order of O((N(F +
1))3) for the inverse of Rrr and O((N(F + 1))2M) for the ma-
trix multiplication in (Rrr)-1hm. For the conjugate gradient
algorithm, there are O {MJ[N(F + 1)]2 + M(5J +1)N(F +1)}
complex multiplications and O {MJ[N(F + 1)]2 +8MJN(F +
1)} complex additions. Usually, J = 5 iterations for the CG
algorithm will suffice for convergence near the DMI solution.
For the FFT-based algorithm, the overall complexity before
Hermitian optimization is O {(N2 +2MN)LF(log2 LF)/2 +
(N3 +MN2)LF}. With the Hermitian optimization, the com-
plexity reduces to O {(N2/2 + 2MN)LF(log2 LF)/2 + (N3 +
MN 2)LF /2}. For the FFT-based algorithm, we usually require
LF ≥ 2F + 1. The complexity is summarized in Table 3. For
simplicity, we only list the most significant part of equivalent
number of complex multiplications. An example is given for
the (4×4) case with F = 10, J = 5. The length of FFT LF = 32
will suffice for both Pedestrian-A and Pedestrian-B channels.
More intriguing information
1. On Social and Market Sanctions in Deterring non Compliance in Pollution Standards2. WP 92 - An overview of women's work and employment in Azerbaijan
3. The name is absent
4. The Economic Value of Basin Protection to Improve the Quality and Reliability of Potable Water Supply: Some Evidence from Ecuador
5. Financial Development and Sectoral Output Growth in 19th Century Germany
6. Initial Public Offerings and Venture Capital in Germany
7. Social Irresponsibility in Management
8. WP 48 - Population ageing in the Netherlands: Demographic and financial arguments for a balanced approach
9. THE ECONOMICS OF COMPETITION IN HEALTH INSURANCE- THE IRISH CASE STUDY.
10. The name is absent