A Note on Costly Sequential Search and Oligopoly Pricing (new title: Truly Costly Sequential Search and Oligopolistic Pricing,)

(a) c = 0.5 and μ = 0.8

Figure 4: The impact of v on expected price (N = 2)

(b) c = 0.05 and μ = 0. 1

d. The effects of an increase in the number of firms N

Under partial participation, it immediately follows from the equilibrium condition v - E [p] - c = 0
that an increase in N does not affect expected price. The underlying economic forces that bring
about this result are, however, less straightforward. We have noted before that Φ(θ ₁; μ; N) is
decreasing in N. This means that without a change in θ1 expected prices would rise: as N increases
it becomes more and more unlikely that an individual firm sells to the shoppers and each firm tends
to concentrate more and more on selling to the non-shoppers. Therefore, expected price would rise
for a given θ1 . Higher expected prices means, however, that a larger fraction of non-shoppers prefers
not to buy and this effect exactly offsets the first effect.

The analysis for the case of full participation follows Stahl (1989) and he shows that expected
prices rise in N . Intuitively, only the first effect discussed above is relevant here as θ1 is fixed to be
equal to 1. In the limit, Stahl (1989) shows that expected price converges to the monopoly price
and the Diamond result holds.

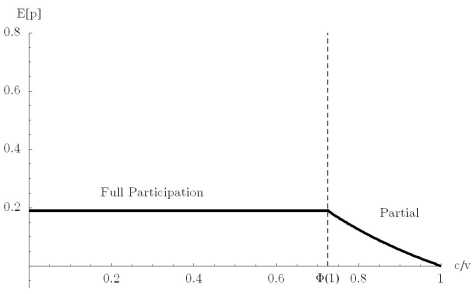
It is then interesting to see which equilibrium arises for which values of N . We will argue that
for given c/v and μ when N becomes sufficiently large, the equilibrium is characterized by partial
participation. What happens as N increases is that, if the non-shoppers keep searching for one
price with probability one, expected price tend to the monopoly price and eventually, the condition
v — E[p] — c > 0 is violated. This is easily seen upon inspection of (10) and noting that Φ(1; μ, N)
declines monotonically with N and converges to zero as N approaches infinity. The implication
of this is that starting from an equilibrium with full participation our model does not yield the

13

<<   11   12   13   14   15   16   17   >>

More intriguing information