where
β0*,t+1=[β0π,t+1-(∑mj=1βuj,t+1)u*]
(9)
and u* is the steady-state unemployment rate, computed as the sample mean.
The conditional variance of steady-state inflation is then given by:
σ^(∏t+ι) = VEt βw‰VEt βt+ι
(10)
where VEtβt'+1
[1-(∑ik=1βiπ,t+1)]-1
Etβ0*,t+1[1-(∑ik=1βiπ,t+1)]
Etβ0*,t+1[1-(∑ik=1βiπ,t+1)]
(11)
is a (k + m + 1 x 1) vector.
Having obtained uncertainty measures for each country, it is possible to analyse the
link between inflation uncertainty and the level of inflation. In particular, we estimate
a bivariate VAR model of inflation and steady-state inflation uncertainty, since the
ECB focuses on long-run price stability. The model also includes a dummy variable to
allow for possible structural breaks in the underlying relationship reflecting the
introduction of the euro.
Specifically, the estimated model is the following:
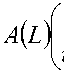
+ BDt +
π
t
unc
<εt √
(11)
where unct+1 represents steady-state uncertainty (i.e. σt2(πt*+1)), Dt is an intercept shift
dummy variable, A(L) a matrix polynomial and B a 2×1 matrix. In the model
specified above, the break date is imposed exogenously to coincide with the
introduction of the euro in December 1998.
Subsequently, we carry out Granger-causality tests and also apply a sequential
dummy approach to detect possible breaks endogenously. The motivation for the
latter type of analysis comes from the literature arguing that rational agents are likely
to react to the announcement of a regime switch before its implementation, and
therefore breaks in the relationship of interest could have occurred before January
1999 (see Wilfling, 2004, and Wilfling and Maennig, 2001) .