good ` in every market equilibrium. We also assume that for any array (α1 , . . . , αn),
the corresponding economy has a unique market equilibrium, up to price normaliza-
tion. These two assumptions are inessential for our argumentation but simplify the
exposition considerably. We shall indicate below which modifications are necessary if
the two assumptions are removed. We consider a market equilibrium and parametric
changes of the bargaining power in household h and obtain:
Proposition 3 (No Spill-overs) With quasi-linear preferences:
(i) A change of αh in a particular household h does not impact on non-members.
∂xk ∂xk
(ii) J,' = J'2 = 0 for all k = 1,...,' - 1.
∂αh ∂αh
(iii) 1 > 0,
∂αh
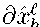
∂αh
< 0.
(iv) Suppose that households are homogeneous with respect to individual utility repre-
sentations and household endowments with wh = w, ∀ h = 1,... ,n. Then:
xhι = αhw + αh uh2 - (1 - αh ) uh 1
xh2 = (1 - αh ) w' + (1 - αh ) uh 1 - αh uh2
The proof of Proposition 3 is given in the appendix. Proposition 3 illustrates that
with quasi-linear preferences, a change of the bargaining power within a particular
household only impacts on the distribution of the num´eraire in household h without
affecting the consumption of the first ` - 1 commodities. A local change of bargaining
power has no price effect and does not affect the utility of individuals in other house-
holds. This also means that a household h cannot manipulate outcomes and possibly
improve utility of household members at the expense of outsiders by misrepresenting
internal bargaining power.
The result is another example of an important line of research that examines in
which circumstances individuals have an incentive to misrepresent their preferences in
the market place. Recently, Makowski, Ostroy and Segal (1999) have comprehensively
characterized continuous, efficient and anonymous incentive compatible mechanisms
and have shown that such mechanisms must be perfectly competitive, i.e. no agent can
change the Walrasian equilibrium price vector by changing his announced preferences.
Quasi-linear preferences are one of the examples that can allow for incentive compatible
mechanisms or perfect competition. Our investigation shows that with quasi-linear
20