Experience, Innovation and Productivity - Empirical Evidence from Italy's Slowdown

Y1 = Y2

H 0: <λ = λ.

^μ1  ^μ2

The third step forward considers the formation of the groups as endogenous. The idea is that firms
introduce innovations because they are more productive, young or intensive at investing into R&D
activities or innovative capital, or maybe because they have more cash flows. The age profile of the
board members and/or the share of temporary workers might be correlated to the innovativeness of
the firms as well.

The new specification for labor productivity growth can be thought of as a standard case of
switching regression model with endogenous switching (as explained firstly in Maddala 1983). We
want to consistently estimate the parameters in two regimes: whether firms are innovative (regime j
= 1) or non innovative (regime j = 2) over the period of observation. The new model specification is
the following.

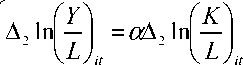
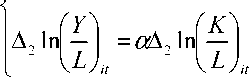
(ТетрогагУ

-----------I + ε_1it if innovative

L √ it-2

(Temporary        . ð

I   + ε_2it if noninnovativ

L     √ it-2

The marginal distribution of the error terms εjit j=1,2 can be assumed normal with zero mean and
constant variance σj². We shall modify this strong assumption in the robustness estimations. The
conditional distribution of the error terms are instead different from zero, according to:

Ε(ε_1it | innovative) ≠ 0

Ε(ε_2it | non innovative) ≠ 0

This is because a criterion function determines whether a firm belongs to regime 1 or 2, as in
equation (7):⁶

'D₁ = 1 if δZ_it + ω_it > 0
1

D₁ = 0 otherwise
⁶ D₁ = 0 ⇔ D₂ = 1 , meaning that, if a firm has not introduced an innovation in 2001-2003, it is non innovative by
definition.

11

<<   10   11   12   13   14   15   16   >>

More intriguing information