Experience, Innovation and Productivity - Empirical Evidence from Italy's Slowdown

We may also allow the parameter of the capital-labor ratio to vary across groups. If this is the case,

the system of equations (9) may be written as:

it

it

∣+ β +γAge + μ(Temporary -σ,^φδZ)+¾,   i∏>, =1

^l.                  I L    J,-2    ^εω Φ(δZ,) ^{1it 1}              (₉')

I + β +Y2 Age, + μ (Tm→∖ .,_τ^φ''Z' + U2it   ifDι= 0

2      2      ,      2                                 εω                           2it               1

^l_lt                    I ^L    Jit-2     ^{1 1-φ}(^δZt )

Clearly, if none of the parameters varies across groups, equation (9) reduces to the simple original

form (4):

₄,Γ Y I *,Γ K I .   . ,       ( Temporary I

Δ 2 Inl — ∣ = ^α ₂lnl — ∣ + ^β + γige_i + μ∖---^t-—∣-    + ^ε_lt

∖^{L j} it            ∖ ^{L j} it                    ∖ ^{L      j} it-2

This is the constrained equation (constraint being equal parameters in all groups) used in the former
Chow test. Leaving aside the potential endogeneity of the capital-labor ratio, the problem of
endogenous group formation in the latter case disappears altogether.

As to the potential endogeneity of the capital stock, we assume that capital accumulation depends
on past investment intensities and initial levels of capital/labor ratio, conditional on size, sector and
group of the firm, whether or not it has introduced innovations, and on firm age. Because of this, we

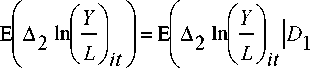
=1

= α∆ ₂ lnl — ∣ + <β₁ + γ1 Age_i + μ1
V L J it I

* P(D₁ = 1) +

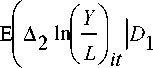
=0 ∣*P(D₁ =0)

TemporaryI

^L    J it-2

Φ(δ z_it )
σ_εω----— (Φ(δ Z_it ) +

^ει^ω Φ(δ z_i ))        ^lt

+ ∖β₂ + Y₂ Agei + μ₂