An Estimated DSGE Model of the Indian Economy.

Nt +1
Vt

S ( Xt )
Yt

Ht - ξβEt [Π .. Ht+1]

Jt - ξβEt [Π^ζ+ι Jt+1]

MCt

^{1 +}^Rt
log At - log At
log Gt ^- log Gt
log MSt - log MS
log RPSt - log RPS
, Λ + Rn,Λ
^log (.τ+‰ )
log Φ t
φEt [log Θ t+ι]

ξeV + (1 - ξe)Di

^{(1 +}^Rk,t)Qt-1 Kt ^-^θt^{(1 +}^Rt⁾⁽^Qt-1 Kt ^- Nt)
^φx⁽^χt ^-^{(1 +} g⁾⁾²

Ct + Gt + It

Yt Λ c,t

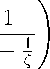
Yt Λ c,tMStMCt

ξ Π^{- -}¹ + (1 - ξ )

W^[

P_t

^{1 +}^Rn,t-1

Pa (log At-1 - log A1-1) + €A,t

Pg (log Gt-1 - log Gt-1) + <G,t

PMS^(log ^MSt-1 ^-^log ^MS) ⁺ €MS,t

Prps^(log ^RpSt-1 ^- log ^rps) ⁺ CRPs,t

1¹ + ^Rn,t- ɪʌ _n, ^θ t _λ , ^φ t

P log ∖ _{1 +} R_n )⁺^θ log Θ ⁺^φ log ¥ ⁺^eMPS,t

logΠ t + τ log Φ t-1

logΘt - (1 - φ) log(Πt)

A.2 StEADy State

The steady state now changes to

Choose a functional form:

vi)

Nt =

(1 - ξe ) D t

( (1 - ξe (1 + Rk))

1 + Rk =

= (¹⁺R ) _s μ K- j

Y? W =

Y_t

1 - α

= ~p—ττ
^Rk ⁺^δ

We obtain χ from econometric studies and we have data on the risk premium Θ = ∖+RR
and leverage (= borrowing/net worth)

KK -1 = _± -1

N nk