which lead to
CU
bl+ι
cu
b i bi
1 + cu
-L- bi
1 + cu
(1 — re) Di
(4)
(5)
(6)
11 11 — reλ
Mi = ----
i V1 + CU J
i
M0
(7)
and therefore
∞
Σ Mi
i=0
Mo
∞ / 1 i ∖ i
=∑ (î—ru
C^U
i=0 ' 7
1 — re
1+cu
1 + cu
I 7
cu + re
(8)
where Mo is the original increase in monetary base, in the currency component.
This alternative derivation of the static multiplier shows its microfoundations
when the behavioural parameters cu and re are constant and homogeneous.
But once we introduce heterogeneity in those individual parameters, the system
changes significantly its behaviour.
To better analyze the importance of heterogeneity, the aggregate description
for the process (4)-(8) must be replaced with a distributed one, where each single
bank and household are represented and explicitly considered. This implies that
in general a closed form solution for the multiplier will not exist, and computer
simulations will be used to gain insights into the behaviour of the system.
2.3 Introducing heterogeneity
In a heterogeneous setting, each bank has its own reserve∕deposit ratio and each
household its own currency∕deposit ratio. If we assume that each agent (bank
or household) in linked to only one agent of the other type, so that the flow
of money is never split into different streams, it is then possible to express the
multiplier (for a unitary increase in the monetary base) as
∞
md = 1 + ∑
i=1
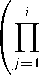
1 — rej
1 + cuj
(9)
where the index i refers to a “round” in the process (i.e., household i deposits
money in bank i; bank i extends a loan to household i + 1, who will deposit
money into bank i+l). A bank or household can be activated in more than one
round during the process, as the index does not identify an agent uniquely, only
the action of an agent.
We can see that if rez = l, or cuz = ∞, for some generic z, then the terms
in (9) for i ≥ z are all zero, because agent z acts as an absorbing state in the