A. Appendix
with 0n P (h)C (h)dh = PHCH. Now combine the preceding equation with the preliminary demand
function from above. Then one gets for C (h):
C(h) = P (h)-θ
PH CH
Ro P(h)1 -θdh
Plugging this into the definition of CH , one gets:
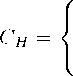
1
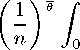
P (h)-θ
PH CH
Ro P(h)1 -θdh
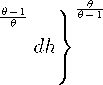
Dividing this formula by CH and raising both sides of the resulting equation to the power of (θ — 1)/θ, I
obtain:
1'∙∙ ndι‰R-rrP^.
θ-1
dh,
which can be solved for PH to finally obtain the domestic PPI given by equation (6):
1 -θ
PH =
Plugging this formula into the last given equation in C (h), one eventually gets equation (10):
PH
θ
CH.
A.2. First Order Conditions for a Utility Maximum
The representative household maximizes
, ,.ʃv--‘ C-'+ X μM∙V-ε γ r--i∏
Ut = ; I -β Pf + 1—ɪШ -'Ls J∫
with respect to the decision variables Ct , Mt , Bt , Lt subject to the intertemporal budget constraint (in
real terms)
Wt Bt-1 Mt-1
— Lt + (1 + it-1) ~P~ + —P—
,Γt(h) c ,Mtdt Bt
+ = Ct + τ∖+ π+τ,'
Hence,
Λt
Et
X β
=t
C1-ρ
—- Ls + (1 + is
P
1)
G9
1-ε
L1-ξ
Γ(h)
])
max
Ct,Mt,Bt,Lt,λt
30
More intriguing information
1. The name is absent2. Auction Design without Commitment
3. The problem of anglophone squint
4. The name is absent
5. The name is absent
6. Better policy analysis with better data. Constructing a Social Accounting Matrix from the European System of National Accounts.
7. Education Research Gender, Education and Development - A Partially Annotated and Selective Bibliography
8. LIMITS OF PUBLIC POLICY EDUCATION
9. The name is absent
10. Segmentación en la era de la globalización: ¿Cómo encontrar un segmento nuevo de mercado?