Estimating the Technology of Cognitive and Noncognitive Skill Formation

characteristics and can be written as

φφφ  φ  φ  φ

τ₁ I₁ + τ₂I₂ + τ₃θ_C,1 + τ₄θ_N,1 + τ₅θ_C,P + τ₆θ_N,P

where τ_i for i = 1,..., 6 depend on the parameters of equations (2.3)-(2.5).¹¹ Cunha and
Heckman (2007) analyze the optimal timing of investment using a special version of the
technology embodied in (2.6).

Let R (Q) = PA=+² (ι+r)^t wQ denote the net present value of the child’s future income
computed with respect to the date of birth, and w is the return per unit Q. Parents have
resources M that they use to invest in period “1”, I₁, and period “2”, I₂. The objective of
the parent is to maximize the net present value of the child’s future income given parental
resource constraints. Assuming an interior solution, that the price of investment in period
“1” is one, the relative price of investment in period “2” is 1/(1 + r), the optimal ratio of
period “1” investment to period “2” investment is

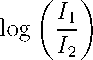
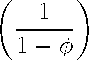
log ( — I — log (1 + r)
τ2

Figure 1 plots the ratio of early to late investment as a function of τ₁∕τ₂ for different values
of φ assuming r = 0. Ceteris paribus, the higher τ₁ relative to τ₂ , the higher first period
investment should be relative to second period investment. The parameters τ₁ and τ₂ are
determined in part by the productivity of investments in producing skills, which are generated
by the technology parameters γ_s,k,3, for s ∈ {1, 2} and k ∈ {C, N}. They also depend on the
relative importance of cognitive skills, ρ, versus noncognitive skills, 1 — ρ, in producing the
adult outcome Q. Ceteris paribus, if T1 > (1 + r), the higher the CES complementarity, (i.e.,
the lower φ), the greater is the ratio of optimal early to late investment. The greater r, the
smaller should be the optimal ratio of early to late investment. In the limit, if investments
complement each other strongly, optimality implies that they should be equal in both periods.

This example builds intuition about the importance of the elasticity of substitution in
determining the optimal timing of lifecycle investments. However, it oversimplifies the anal-
ysis of skill formation. It is implausible that the elasticity of substitution between skills in
producing adult outcomes ( ₁ ¹, ) is the same as the elasticity of substitution between inputs
-φQ

in producing skills, and that a common elasticity of substitution governs the productivity of
inputs in producing both cognitive and noncognitive skills.

Our analysis allows for multiple adult outcomes and multiple skills. We allow the elastici-
ties of substitution governing the technologies for producing cognitive and noncognitive skills

¹¹See Web Appendix 1 for the derivation of this expression in terms of the parameters of equations (2.3)-
(2.5).

<<   5   6   7   8   9   10   11   >>

More intriguing information