Expectation Formation and Endogenous Fluctuations in Aggregate Demand

Divergence Regime

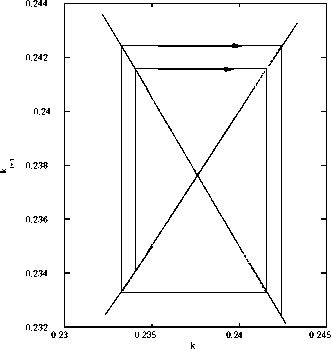
Figure 4: The Evolution of Physical Capital in Convergence and Divergence
Regimes.

Convergence Regime

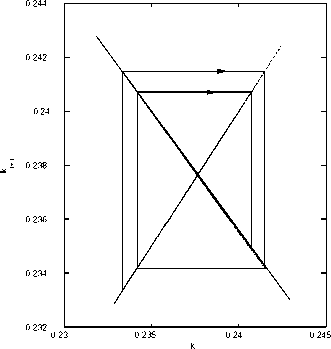
It is relatively straight forward to establish that as long as ψ > 1 the economy
does not settle down into a steady state. The reasoning is simple and assumes
first the opposite. If the economy were to settle into a steady state then at
some point the predictor would become relatively efficient and errors made with
the predictor and their variance would be arbitrarily close to zero. Therefore,
learning would become suboptimal and the quality of signal chosen would be
eventually zero, i.e., q2 = 0. However, with qj set to zero x_t would follow a
divergent path and no rest point would be attained. Hence a contradiction. It
remains to establish that dynamic variables will not grow or keep diminishing
for ever, i.e., it needs to be shown that the lack of a steady state implies equilib-
rium oscillations. In economic terms variable x_t+ι cannot grow for ever for its
growth requires on one hand high investment as x_t+ι = 2ψ⅛_t+ι ,i.e., future prof-
its are increasing in the productive capacity of the economy, and on the other
hand discourages investment as indicated by equation (32) high expected future
income leads to small savings. Similar argument applies to the case when x_t+ι
where to keep falling. Technically, the eigenvalue in the system (??) is negative
hence the path the economy follows must be oscillatory.

In general the dynamic properties of the process followed by x_t depend on the
magnitude of the coefficient preceding x_t. For q_t² sufficiently high the coefficient
is necessarily less than one and x_t converges to an equilibrium. On the other
hand if q2 is close to zero then the coefficient is higher than one and x_t does not
converge to an equilibrium. Therefore, depending on the magnitude of q_t² the
economy follows either a divergent or a convergent path. Naturally, q_t² is chosen
in equilibrium and the equilibrium choice determines the characteristics of the
underlying equilibrium process. Observe that whenever the economy follows a

21

<<   18   19   20   21   22   23   24   >>

More intriguing information