A MARKOVIAN APPROXIMATED SOLUTION TO A PORTFOLIO MANAGEMENT PROBLEM

J(τ, х; и) =

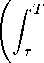
g(X(t),_u(t),t)dt + s(X(T))

∣X(τ) = х

is the profit-to-go function. For Markovian feed-
back controls the maximum value of (4)

H(τ,x) = max J(τ, x; μ(∙))
μ(∙)

satisfies the HJB equation

max{ρ(x, u,t) + L_uH(t,x)} = 0    (5)

with the boundary condition

H(T, X(T)) = s(X (T))        (6)

where L_u is the operator

Q      n                  .ɔ

^£“ ⁼ ^ ⁺ §^/i(æ,w’^Tfe

I A _π , _λ ∂²

+ - > B_{i j}(x,u,τ)-—-—      (7)

²_i~'₁            ∂x_i∂x_j ^{v 7}

and where /, is the г-th component function of
/ and Bij is the i,J-th entry of the covariance
matrix B = bb^τ.

2.2 A Corresponding Markov Decision Chain

A Markov decision chain corresponding to the
optimisation problem max(4) subject to (1) and
(2) is obtained through the following three steps.
First, the state equation (1) is discretised in
time using the Euler-Maruyama approximation
(see [5]). Then, the state space is restricted to a
finite dimensional discrete state grid and, finally,
the transition probabilities and rewards for these
discrete states are specified.

Euler-Maruyama Approximation. An Euler-
Maruyama approximation of process⁴ X C IR¹
that satisfies equation (1) is a stochastic process

γ = {Y_i ex, o<i<N}

satisfying the equation (called the iterative scheme)

Y_f+ι = Y_i + f (Y_i, u_i, τ_i) (τ⅛₊ι - τ_i) +
b(Y_i, u_i, τ_i) (W(τ_i+1) - W(τ_i)) (8)
τ ⁼ ! o }<-o∙ with ⁷^o = O and Tjv = T is a strictly
increasing sequence of real numbers that partition
the time interval [0,T].

The indices run t = 0,1,2,..., N — 1, the initial
and subsequent values are, respectively

У о = X(O) = x₀, Y_i = Y(τ_i). (9)

For a time discretisation using a constant time
step (where N is a positive integral number)

„ _{c 1}                              T        _{f λ}

τ_i = t δ where δ = τ_i+-_i — τ_i = —.    (10)

Notation. The discretisation scheme, while intu-
itively simple, overlays several layers of discretisa-
tion: of time, of state, and of noise. We adopt the
following conventions.

(1) Continuous-time variables: x(t) (standard);
variables in discrete time: x_i.

(2) Points of the discrete state space (“grid”)
x ∈ X_i.

(3) Stochastic processes: x (bold).

Discrete State Space. Equidistant grids will be
used for simplicity (see [8]). The discrete state
space for stage t is denoted by X_i C IR¹. Let
the upper and lower bounds of the state grid be

U_i = max X_i and L_i = min X_i.

respectively. A point x ∈ X is defined to be within
the grid X_i if L_i ≤ x ≤ U_i. The collection of the
discrete state spaces for all the stages, {A√})Σ₀,
is denoted X and called the discrete state space.

Adjacency. Heuristically, the scheme approxi-
mates a point of X at stage I by the points of
X_i which are “adjacent” to it.

(1) Two states of X_i are adjacent if no other
state of X_i lies between them ⁵ .

(2) Given a point of the continuous state space,
x e X, a pair of states, x^θ ∈ X_i and
x® ∈ X_i, is adjacent to x if the states are
adjacent and x^θ < x < x^φ.

(3) Given x ∈ X with x > U_i define U_i to be
adjacent to x.

(4) Given x ∈ X with x < L_i define L_i to be
adjacent to x.

(5) Given x ∈ X with x ∈ X_i define x to be
adjacent to itself.

⁴ The approximation scheme is introduced for a one di-
mensional process. The extension of the scheme to IRⁿ is
obvious.

⁵ In IRⁿ two states are adjacent if their projections onto
each of the n coordinate axes are adjacent in the sense just
defined.

<<   <   1   2   3   4   5   6   >   >>