Density Estimation and Combination under Model Ambiguity

(61)

E [J_n(xi,xj)J_n(xj ,xi)]

' 4-_h( K²(u)du + o(h) = O(h).
4h             h h

(62)

and

E H1²n (xi

xj)^∖ = E ^£2J_n (xi,xj)+ J_n (xi,xj)J_n (xj ,xi

)1 = h/

K ²(u)du + o(ɪ) = θ(ɪ),
hh

(63)

21
^σ2n = n2h J K^{2(u)du + o(}h).

(64)

The second term in () is the expected value of a Bias term, that is

Bbn ¹ X bn(xi) ' h-μ₂ I g(²∖x')dx + o(h²),
n2

i

(65)

where g(²)(x) is the second derivative of the p.d.f. Hence Bb_n = Op (n ^1/2h²^ Thus, what we obtain is

^ ^ ^

V1n = V11n + Bn

^σ1nN^{(0, 1}) ⁺ y μ2

g⁽²⁾(x)dx+o(h²).

(66)

1

V2n = —
n
i

"p"" /   ∖      P/ ∖

fn(xi) — f(xi)

g(xi)

—                "I 2

₊ ^{f (}xi) ^- g⁽xi)
g(χi)

f fn(xi) — f (xi)

∖     g⁽xi)

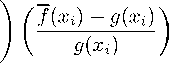
(67)

= V^b21n + V^b22n + V^b23n.                                         (68)

V21n = ¹ X
n

i

2

—1— X an(xi,Xj) I
n—1

j,i6=j

1

n(n — 1)²

ΣΣаП (xi,xj )+ ₍ ⅛_π∑ ∑∑^αn(xi>Xj )αn(xi,xz ).
n(n — 1)

i j,i6=j                              i j6=i z6=j

(69)

The first part is a variance term and it will affect the mean of the asymptotic distribution. The second
term equals a twice centered degenerate U-statistic U2_n, which is of the same order of magnitude of V11_n
and it also affects the asymptotic distribution of KI.

27